과제 목표
두 개의 rectified image를 통해서 epipolar line 얻기
1) Fundamental Matrix Estimation
2) Compute epipoles
3) Epipolar lines
간단 용어 설명
동차좌표(Homogeneous coordinates)
n차원 공간을 n+1차원의 좌표로 나타내는 좌표계
스테레오(Streo)
: 같은 물체에 대해 서로 다른 장소에서 촬영한 여러 이미지에서 물체의 3차원 정보를 계산하는 학문
간단히 말해서 서로 다른 장소에서 촬영한 두 장의 이미지에서 거리 정보를 추출해 내는 분야
예를 들어 캐치볼을 할 때 한 쪽 눈을 감고 하면 거리계산이 어려운 것과 마찬가지로 이미지를 보고 거리 계산을 하기 위해서는 두 개의 이미지가 필요
디스패리티(disparity)
: 이미지에서의 어떤 포이트가 다른 이미지에서 매칭되는 점과의 차이
카메라 간에 거리가 멀면 디스패리티가 크게 나타남 -> 거리 정보를 정밀하게 파악 가능
에피폴(epipole)

: 3차원에는 X라는 점 존재한다. 이 점은 왼쪽 카메라에서 렌즈의 초점 O와 연결하는 직선,레이(ray) 상에 놓여 x라는 도메인에 투영된다. 우리가 이미지에서 확인한 x 라는 점은 3차원 공간 상에서 X이기도 하지만 xX(=oX) 선분위에 있는 어떠한 점도 이미지 상에서는 x로 보이게 된다. 이는 투영(projection) 되었기 때문에 거리 정보가 사라진다는 걸 직관적으로 느낄 수 있는 부분이다. 그러므로 xX선분 상에서 x는 어떤 점이든지 될 수 있기 때문에 x 에 대응되는 오른쪽 카메라에서 후보가 되는 여러 x가 x' 도메인 상에서 선분으로 표시가 되게 된다. 이때 이 선분들이 하나로 만나는 점이 생기는데 이 점은 두 카메라를 연결한 OO' 선분이 이미지를 관통하는 점으로 e 와 e' 로 나타난다. 이 e 를 에피폴(epipole)이라고 부르고 이 epipole 을 지나는 후보군 선분을 에피폴라 라인(epipolar line)이라고 부르게 된다.
간단히 말해서 두 카메라 중심 이은 선분과 이미지 도메인이 만나는 점은 에피폴이라고 하고 x 의 후보군과 이미지를 통과하는 점을 에피폴과 잇은 선분을 에피폴라 라인이라고 한다.
-> X까지의 거리정보가 없을 경우, x 도메인에 X 좌표를 B의 한 좌표로 완벽하게 결정할 수 없지만 에피폴라라인을 계산할 수 있는데 이때 사용되는 변환 행렬이 Fundamental Matrix, Essential Matrix이다. Epipolar Geometry 에서는 서로 다른 두 시점에서 찍은 이미지들의 좌표 사이에 변환 행렬들을 매개로 하는 변환 관계가 성립하는데 이를 바탕으로 기하하적 문제를 풀게된다.
Fundamental Matrix
: Essential Matrix는 정규화된 이미지 평면에서의 매칭 쌍들 사이의 기하하적 관계를 설명하는 행렬이다. 카메라 내부 파라미터 행렬인 K가 제거된 좌표계에서의 변환 관계이다. 그에 반해 Fundamental matrix는 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀(pixel) 좌표 사이의 기하학적 관계를 표현하는 행렬이다.


임의의 두 이미지에 대해 매칭되는 x2,x1 사이에는 항상 다음과 같은 관계를 만족하는 행렬 F가 존재하고 이러한 행렬 F 를 Fundamental matrix 라 부른다.
특이값 분해(SVD, Singular Value Decomposition)
: 특이값 분해는 임의의 m x n 차원의 행렬 A에 대하여 다음과 같이 행렬을 분해할 수 있다는 행렬 분해 방법 중 하나이다.
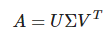
여기서 네 행렬()의 크기(혹은 차원)와 성질은 다음과 같다.
: rectangular matrix, 직사각 행렬
: orthogonal matrix, 직교 행렬
: diagonal matrix, 직사각대각행렬
: orthogonal matrix, 직교행렬

OpenCV 관련 함수
1) findFundamentalMat() : 두 이미지 사이의 fundamental matrix 계산하여 반환, 입력으로는 8쌍 이상의 매칭 이미지 좌표쌍 입력
과제 분석
1. Fundamental Matrix Estimation
두 개의 rectified images 를 사용한다.
이에 대한 .npy 파일을 제공한다. 이는 numpy 배열를 외부 파일로 저장한 것이다.
각 점은 3 x N의 동차 좌표로 제공된다.
Fundamental Matrix은 아래와 같이 정의 된다.
x', x는 이미지이다.

아래와 같이 정의 될 경우 아래의 식이 성립하게 된다.



이 문제에서는 8 point algorithm을 통해서 fundamental matrix 를 계산한다. 원래는 8개의 점을 사용하지만 여기서 8개보다 많은 걸 쓰기 때문에 overdetermined 가 일어날 수 있다. 그래서 least square solution을 사용한다.
SVD를 통해서 rank(F)=2 를 확인한다.



참고자료
[13호]스테레오 영상을 처리하는데 있어 발생하는 이슈 | NTREXGO - 디바이스마트, 엔티렉스 컨텐츠
스테레오 영상을 처리하는데 있어 발생하는 이슈 글 | 위드로봇(주) 김도윤 ■ 스테레오 비전이란? 영화관에서 3D나 4D라는 표현이 자주 쓰이게 되면서 입체감 있는 영상에 대한 이해는 예전보다
www.ntrexgo.com
[영상 Geometry #7] Epipolar Geometry
(3D 비전 geometry 마지막 6번째 파트 epipolar geometry입니다) 6장 epipolar geometry를 마지막으로 '영상 geometry' 글을 마무리하고자 합니다. 6. Epipolar Geometry Epipolar geometry는 스테레오 비전(stere..
darkpgmr.tistory.com
Python 넘파이 배열 값 추가하기 ndarray
파이썬에서 array는 append 메서드를 사용해서 배열을 추가할 수 있습니다. append 예제 arr = [] arr.append([1, 2, 3]) arr.append([4, 5]) print(arr) 결과 [[1, 2, 3], [4, 5]] 행 길이는 다르지만 2차원 배..
ponyozzang.tistory.com
파이썬 numpy - array 사칙연산, 행렬 곱, Broadcasting
파이썬 numpy의 array 사칙연산 및 행렬 계산을 공부하면서 정리한 글입니다. 사칙연산 numpy는 기본적으로 array 간의 사칙연산을 지원합니다. 행과 열이 같은 배열을 계산하면 값은 위치에 있는 값
firework-ham.tistory.com
github.com/marktao99/python/blob/master/CVP/samples/sfm.py
marktao99/python
Contribute to marktao99/python development by creating an account on GitHub.
github.com
nbviewer.jupyter.org/github/BonJovi1/Epipolar-Geometry/blob/master/code.ipynb
코드 확인
https://github.com/Chung-god/ComputerVision/tree/main/Epipolar
Chung-god/ComputerVision
Using Python. Contribute to Chung-god/ComputerVision development by creating an account on GitHub.
github.com
결과물
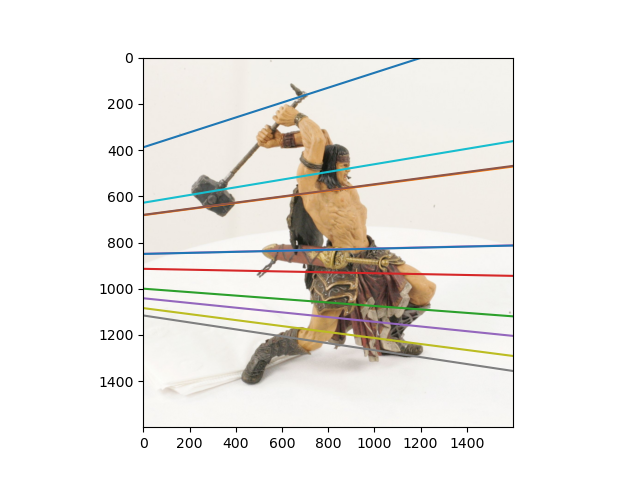
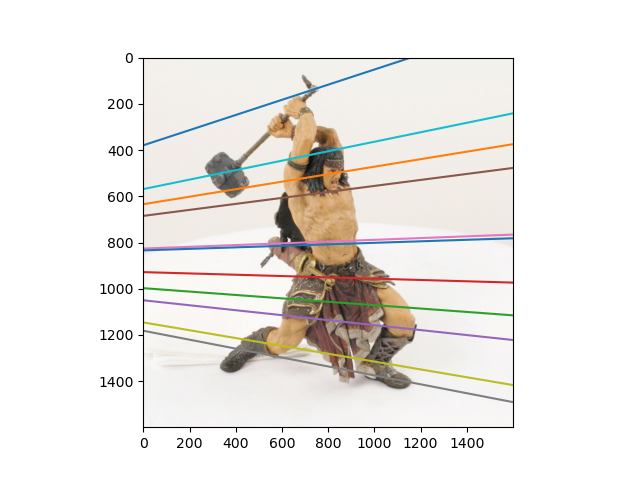
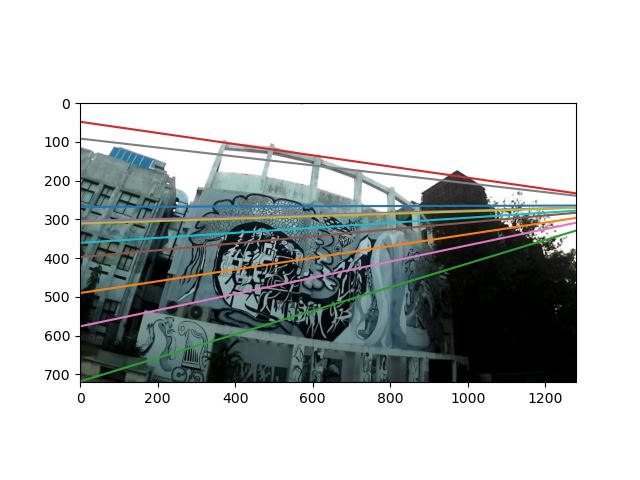
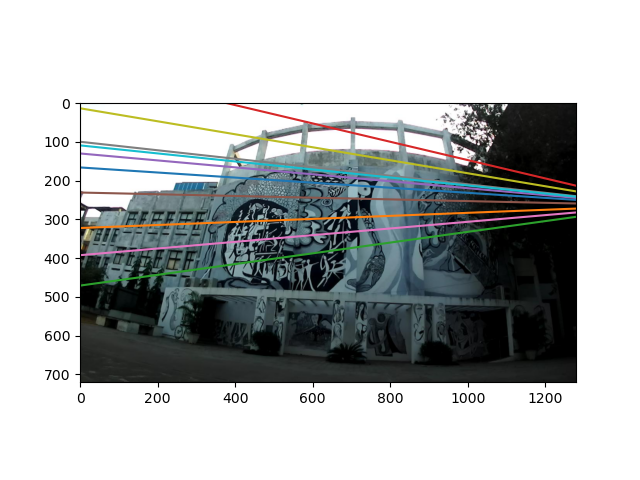
'공부 > 컴퓨터비젼' 카테고리의 다른 글
| [컴퓨터비전 과제] 7. CNN(Convolution Neural Network) (0) | 2021.06.10 |
|---|---|
| [컴퓨터비젼 과제] 6. SVM(Support Vector Machine) (0) | 2021.05.27 |
| [컴퓨터비젼] 13. Stereo (0) | 2021.04.18 |
| [컴퓨터 비젼] 11.Single-View Modeling (0) | 2021.04.18 |
| [컴퓨터 비젼] SIFT(Scale Invariant Feature Transform (1) | 2021.04.12 |


