불확실성을 표현할 확률이 어떻게 인공지능에 적용을 될지에 대해서 이야기 해보겠습니다.
목차는 다음과 같습니다.
- Basic Probability Notation
- Language of Propositions in Probability Assertions
- Inference Using Full Joint Distributions
- Independence
- Bayes' Rule and Its Use
Basic Probability Notation
가장 먼저 set 오메가로 시작합니다. 이를 sample space 라고 부릅니다.
ex) 주사위 굴리면 6개의 경우의 수가 나옴 -> 6개의 sample space
그리고 6개의 숫자 하나하나를 sample point/possible world/atomic event 등으로 부릅니다. (단어를 알고 있자)
Probability space or Probability model
: sample space 가 확률값을 가지게 될 때 , 주어진 확률값은 P(w) 로 표현하게 됩니다. 아래 내용은 고등수학에서 벗어나지 않죠?
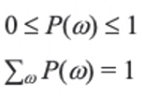
event A가 발생할 가능성은 atomic event 를 더해주면 됩니다. (3이나 4가 나올 확률)
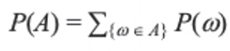
Language of Propositions in Probability Assertions
Random Variable
각각의 sample points 가 어떠한 range (실수, 불리안 등등)로 맵핑이 되는 함수입니다.
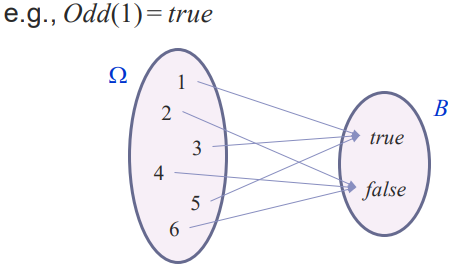
여기서 Odd(n) 이 random variable 이라고 할 수 있겠죠.
이 부분도 고등학교 수학인데요. 여기서 X는 랜덤 변수이고 x 는 이 랜덤 변수의 값입니다. 여기서는 true/false 겠죠. 이 값이 나오는 Probability 의 모든 합을 합친거죠.

세 가지 종류의 random variable 이 존재를 합니다.
1) Boolean
ex) Cavity(do I have a cavity? = 충치가 있나요?)
Cavity = true(false)
여기서 주의할 건 대문자 Cavity 를 쓰는거죠. 대문자로 쓰는것이 random varible 이고 소문자도 함축한다는 의미입니다.
2) Discrete (finite or infinite)
ex) 날씨는 <맑음, 비,구름,눈> 중 하나
필드는 무한할 수 도 있고 제한적일수도 있습니다.
이 들이 맵핑이 될때는 서로 겹치지 않습니다.
Weather = rain 은 proposition
3) Continuous (bounded or unbounded)
바운드가 있을 수도 있고 없을 수도 있습니다.
ex) Temp = 21.6 이보다는 이렇게 표현하는 것이 좋습니다. Temp < 22.0
그리고 다음과 같이 여러개의 basic propositions 이 합쳐져서 하나의 propositions이 될 수도 있습니다.
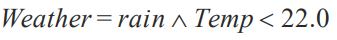
다음은 중요한 용어인 Prior of propositions 또는 unconditional probablilities of propositions 을 살펴보겠습니다.
앞서서 다음과 같은 propositions 을 봤었죠.

이러한 probability 계산을 하는데 있어서 새로운 정보, 즉 evidence 가 도착하기 전에(prior) 믿음을 Prior, 그리고 condition이 있는 상황이 아닌거니깐 unconditional 입니다. 아무런 조건 없는 믿음이니깐요.
Probalility distribution 은 random variable 이 있을 때 모든 가능한 assignment 값을 제공을 하는 겁니다. 예를 들어 다음과 같은 거죠. 날씨는 위에서 들었던 예와 같이 <맑음, 비,구름,눈>으로 4개가 있죠.
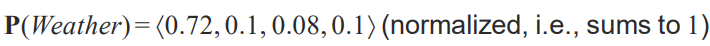
각각의 가능성을 나열한 모습입니다. 그리고 모두 합했을 때 1이 나와야합니다.
이것이 보편적이긴 하지만 앞에서 말했듯이 확률이 늘 같은 random variable 을 가지는 것은 아닙니다. 그래서 복수의 random variable 에 대한 확률 sets을 'Joint probability distribution' 라고 합니다. 예를 들어 볼까요? 다음 그림을 보면 쉽게 이해가 되실 겁니다.

Probability for continuous variables
: probability distribution을 파라미터가 있는 함수로 표현을 할 수가 있습니다.
그래야 continuous 하게 할 수 있겠죠. 간단한 예를 uniform density 를 보겠습니다.
P(X=x) = U[18,26](x)
범위를 U[18,26] 처럼 파라미터가 있는 함수로 표현할 수 있는 겁니다. 여기서는 18과 26 사이에 값이 존재한다는 의미입니다.
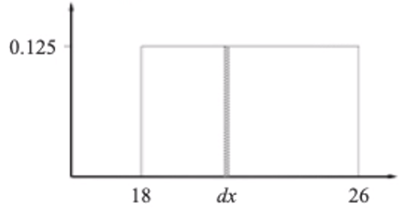
범위가 8이니깐 이 값을 다 합쳤을 때는 1이 되어야함으로 0.125 입니다.
이처럼 모든 x 를 정의할 수 있습니다.
Continuous random variable 입니다.

위 그림을 보면 두개의 같지만 다른 표현이 있습니다. 이렇게 표현하는 경우도 있다는 것을 알아두면 됩니다.
uniform 뿐만 아니라 Gaussian 같은 경우도 있죠. 이를 통해 Probability Distribution 을 수행하는 경우가 많고 자주 등장을 할 예정입니다.
이번에 또 중요한 단어인 'Posterior Probabilities' 에 대해 배워보겠습니다. Conditional 이라고 불리기도 합니다. Prior 에 반하는 거란 느낌이 오시나요? 예를 들어 보겠습니다. 아래는 toothache 가 true 일 경우 cavity 가 true 일 확률이 0.8이라는 말이죠. 이게 조건부 확률이었나요? (고등학교 졸업한지 3년)

여기서 우리가 알고 있는건 toothache 가 true 라는 condition 입니다. 여기서 주의할 점은 '만약 치통이 있으면 80퍼의 확률로 충치가 있다 = if toothache then 80% chance of cavity' 가 아니라는 점입니다. if~ then 을 쓰는 것은 앞에서 본 logic 의 개념이기 때문입니다. 이런 미묘한 차이가 엄청난 차이를 나타냅니다. 그리고 더 많은 evidence 가 주어지면 초반의 belief 가 감소합니다. 즉 항상 유용하지는 못한다는 거죠. 극단적인 예시이긴 하지만 아래의 경우 cavity가 true 라는 evidence 가 추가가 됨으로써 믿음이 완전이 사라졌죠. 그냥 사실이니깐요!
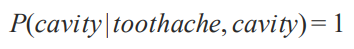
물론 항상 믿음이 더 사라지지는 않겠죠. 또 극단적인 예시로 아래처럼 49ersWin 팀이 승리를 했다는 evidence 가 들어 오면 이건 충치와 전혀 관계가 없죠. 그럼으로 이는 확률을 더 복잡하게 만드는 겁니다. 독립적인 거죠. 이런건 제거를 하고 간단하게 문제를 바꿔줄 줄 알아야합니다. 즉 늘 evidence 가 많다고 좋은 것은 아닙니다!
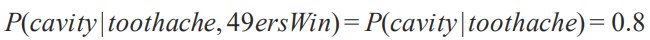
이 부분은 중요한 부분이기 때문에 계속 이야기를 하게 될 것입니다.
Conditional probability를 수학적으로 나타내보면 다음과 같습니다.

random variable을 chain rule 로 여러번 연결할 수도 있습니다.
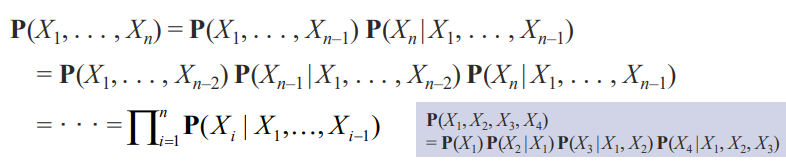
Inference Using Full Joint Distributions
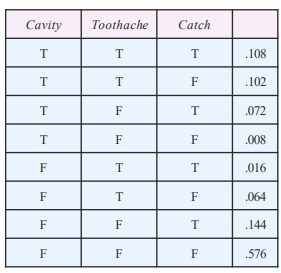
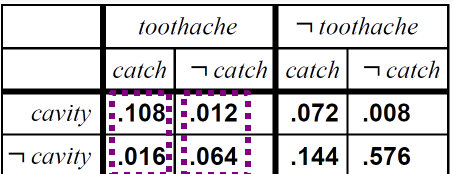
다음 세개의 random variable 로 구성된 Joint distributions 의 예인 표가 있습니다. Catch는 충치 검사라고 생각을 합시다.
이를 다음과 같이 도식화 해봅시다.
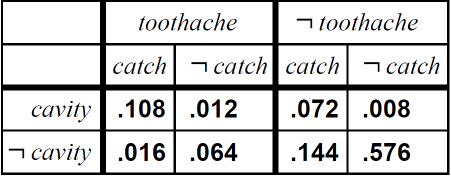
세부화 하여 총 8개의 경우를 표현한다는 것을 알 수 있죠.
만약 어떠한 proposition 파이에 대해 수학적으로 나타내고 싶다면 다음과 같이 쓸 수 있습니다.

파이가 이벤트라고 봤을 때 이에 해당되는 atomic event 의 합이라는 의미이죠
예를 들어 P(toothache) = 0.108 + 0.012 + 0.016 + 0.064 = 0.2 이겠죠?
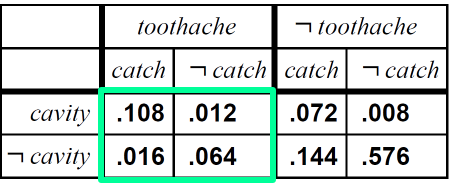
아래도 마찬가지인 경우입니다.
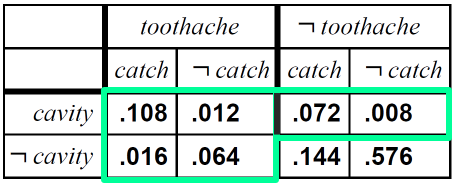

contitional probabilities 에 대해서도 계산이 가능합니다. toothache 가 true 일 때 cavity 가 false 일 확률을 구해라라는 의미이죠?

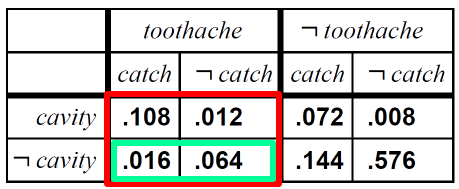
적혀져있다고 늘 확률을 구해야하는 건 아닙니다. 아래와 같은 경우도 존재하겠죠.
여기서 콤마(,) 는 and 의 의미를 가지고 있습니다.
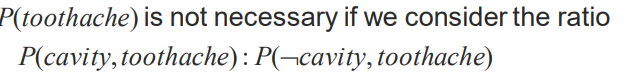
자 이번에는 Conditional Probability가 아닌 Conditional Distribution을 나타낸겁니다. 볼드체로 쓰면 Distribution입니다.
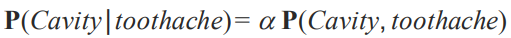

normalization constant 알파를 사용하면 됩니다. 이게 무엇을 의미하냐면 저희가 계산해야하는 것은 Cavity 가 false 일때 Cavity 가 true일 때의 확률 인 거 입니다. 결론만 보자면 다음과 같죠
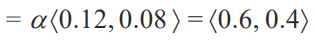
이는 P(Cavity,toothache) 의 값만 먼저 구한 겁니다. 분자 부분이죠. 여기에 P(toothache)를 나누면 0.6,0.4 라는 값이 나오지만 이를 모르더라하더라도 <0.12,0.08> 의 합이 1이어야하는 사실을 알기 때문에, 그렇게 해주는 Normalization constant 알파를 구하면 된다는 거죠. 정리를 다시 하자면 P(toothache) 값을 구하지 않아도 P(Cavity,toothache) 값을 구해서 비율로 합이 1이 되도록 하는 알파를 구하면 되는거죠.
0.12 + 0.08 = 0.2
'5를 곱하면 1이 되겠네. 아 알파는 5구나'
<0.12 * 5 , 0.08 * 5 > = <0.6, 0.4>
중간과정을 다음과 같습니다.

보면 기준은 Cavity 인것을 알 수있죠. 대문자로 판단하면 됩니다. 두번째 등호 줄에는 toothache 와 catch가 true일때 cavity 가 true/false 인 값 0.108과 0.016을 구했다는 것을 볼 수 있죠. 0.012, 0.064 는 not catch 부분입니다.
이 아이디어를 좀 더 수학적으로 표현해보자면 marginalization 또는 summing out rule 이라고 합니다.
Y,Z라는 두개의 set 이 있을 때 Y set 에 대한 Probability Distribution 을 구해보면 다른 변수인 (여기서는 Z) 에 관한 모든 가능성 있는 값을 계산해서 구한다는 겁니다.
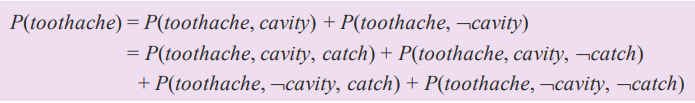
이와 유사하게 Conditioning rule 을 쓸 수 있습니다.
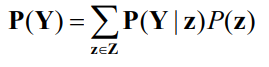
Y에 대한 distribution을 z 가 발생했을 때 condition distribution 그리고 z 에 대한 probability 이렇게 Conditioning rule 을 써서 생략된 모든 z 에 대해서 고려를 해서 정리를 하면 똑같은 결과를 얻을 수 있습니다. 참고하시면 됩니다.
따라서 X을 알고 있는 Joint Distributions 이 주어졌을 때 모든 변수의 집합이라고 생각해봅시다.
이때 query variables Y 가 주어지고 이에 대한 posterior joint distribution을 구하고 싶다.
라고 했을 때 주어진 조건이 evidence avriables E 에 구체적인 e 라는 값을 주는 겁니다.
여기서는 하나의 변수라는 의미들이 아니라 set 이라는 의미입니다.
여기서 숨겨진 변수인 Hidden variables 을 H 라고 합시다. H = X - Y - E 입니다.
결국 joint entries 에 required summation 은 hidden variables 에 대해서 summation 을 함으로 계산을 할 수 있는 겁니다. 수학적으로 나타내면 다음과 같습니다.

이렇게 Joint Distributions을 쓰게 되면 분명한 문제가 생깁니다. 어떠한 query, proposition이 주어지더라도 답을 할 수 있다는 장점이 있었지만 현실적으로 이러한 Full Joint Distributions을 적용할 수 없게 되어있습니다. time complexity 을 고려하게 되면 최악의 경우 O(d^n)입니다. 공간복잡도도 동일합니다. 따라서 현실 상황에서는 random varible 이 두 세개가 아닌 수백 수천개가 등장할 수 있기 때문에 지수단위로 증가하는 걸 사용하기는 힘듭니다.
이를 완화하기 위한 방법이 'Independence'라는 방법입니다.
Independence
예를 두개의 변수 A,B 라는 게 주어지고 이게 독립일 때 이 둘의 확률은 상관이 없다는 의미입니다. (고등학교 때 배운 거죠.)
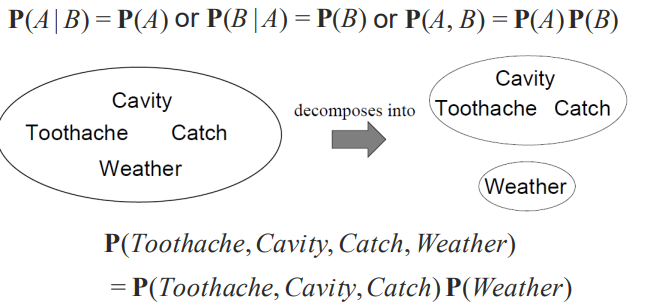
P(Toothache,Cavity,Catch,Weather) 을 계산하면 32 개의 entries 가 나오는 데 독립을 이용하면 12 개로 줄일 수 있습니다. biased coin 의 경우에는 (모두가 독립일 경우) 2^n -> n 인거죠. 문제는 이런 독립이 효율적이지만 드물다는 거죠.
어떻게 해야할까요? 일단 독립이라는 걸 확인할려면 다음의 식이 성립해야합니다.
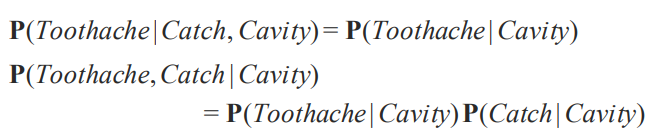
이번에는 chain rule 을 사용해서 full joint distribution을 쪼개보도록 합시다.
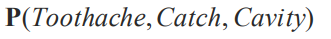
첫번째 변수에 대해서 나머지 변수를 Condition으로 둡니다.
그리고 두번째 변수에 대해서 진행합니다.

그러면 총 세 개의 Distribution으로 생각해볼 수 있을 겁니다.
그럼 여기서 저희가 생각할 수 있는 entries 의 수를 봅시다.
첫번째로
3개의 독립을 고려를 안 했을 때 여기서 생각할 수 있는 독립된 엔트리 수는 7개 였습니다.
그러면 chain rule 을 쓰고 Conditional independence 를 적용을 했을 때는 어떨까요?
합이 1이라는 것을 이용을 해서 그런 부분을 다 제거합니다. 그래서 만약에 첫번째에 대해서 생각을 해보면은 만약 Cavity 가 true일때 Toothache 가 true/false 가 있는데 true 만 계산하면 나머지는 1 - 로 계산을 할 수 있습니다. 그래서 toothache 가 true 일때 Cavity 가 true 일때 를 계산하면 나머지를 계산할 수 있기 때문에 2개의 독립적인 엔트리가 나올 겁니다. 나머지도 똑같습니다만 마지막의 P(Cavity) 는 true 하나입니다. 이렇게 5개의 엔트리입니다. 7개에서 5개로 줄어든 거죠. 변수에 수가 많아진다면 더 효과가 크게 보이겠죠.
즉 Conditional independence 는 불확실한 상황에서 지식을 기본적이고 현실적으로 받아들일 수 있는 방식인 겁니다.
Bayes' Rule and Its Use
이어서 베이스 룰에 대해 간단하게 이야기 해봅시다. 간단히 Product rule로 Bayes' Rule을 나타낼 수 있습니다.

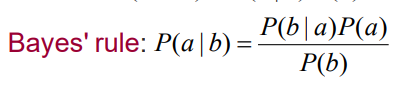
크게 특별한 것은 없습니다. 이를 어떻게 사용할 수 있을 까요? 이를 distribution form 으로 나타낼 수 있습니다.
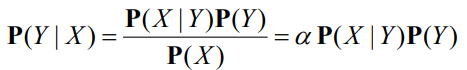
전체의 합이 1인 것을 알기 때문에 알파로 표시합니다. 이러한 베이스룰이 어디에 유용한 것 일까요?
저희가 알고 싶은 확률은 diagnostic 확률, 즉 진단하고 싶은 확률입니다. 또 causal probability 가 존재하죠. 이는 원인과 결과가 있는 순방향의 확률입니다. diagnostic 은 원인에서 결과가 아니라 결과에서 원인으로 역추적하는 거죠. 직관적으로 생각해도 결과를 알고 원인을 아는 것은 어려운 문제입니다. 즉 diagnostic 문제를 Bayes' Rule 을 써서 더 쉽게 원인에서 결과를 얻는 문제로 바꿔버리는거죠.

즉 더 쉬운 문제로 바꾸어주는 겁니다.
Bayes' rule 과 앞에서 배운 conditional independence를 합치면 더 흥미로운 결과를 낼 수 있습니다.
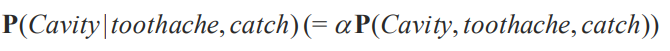
여기서 원인과 결과를 생각해봅시다. toothache, catch 가 있을 때 충치일 확률을 구하는 건 매우 어려운 문제라는 것이죠. 그래서 원인과 결과를 뒤집어버립니다.

여기서 저희가 conditional independence를 사용하는 겁니다. 즉 toothache 와 catch 가 연관성이 없는거죠.

'공부 > 인공지능' 카테고리의 다른 글
| [인공지능]10.Bayesian Networks 2 (1) | 2020.12.07 |
|---|---|
| [인공지능] 9.Bayesian Networks (0) | 2020.10.16 |
| [인공지능] 7.Knowlege Representation (0) | 2020.10.15 |
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |
| [인공지능] 5.Continuous State Spaces & Constrained Optimization Problem (0) | 2020.10.14 |



