Continuous State Spaces
- Gradient methods attempt to use the gradient of the landscape to maximize/minimize f by

저번 게시물에서는 'Hill Climbing' 이 나왔었습니다. 이는 'Gradient descent/ascent'라고도 불린다고 했습니다. 이 Gradient method 에 관해서 더 알아보도록 하겠습니다. 참고로 Gradient 는 기울기라는 뜻입니다. 앞에서 살펴봤던 문제들 중에서 TSP(외판원 문제), N-queens 들 같은 경우 object function 을 주어진 state 에서 '총 거리가 얼마인지' 와 같이 계산을 할 수 있었습니다. 그 중에서도 Local Search 에 Hill Climbing 은 주변에 이웃을 보고 object function의 값이 제일 커지거나 작아지는 State(Neighbor) 로 이동을 하였습니다. 특히 steepest 버전이 이와 같이 동작을 하게 됩니다.
하지만 이번에는 그런 object function이 Continuous(연속적인) 함수로 주어진 것입니다. 그랬을 때 주변에 state 에 목적 함수 f(x) 를 계속 계산할 필요가 있을까요? 생각해보면 그러는 게 맞지 않나 싶으시겠지만 그럴 필요가 없습니다.
즉 Continuous function f 에 대해서 미분 가능하다면 기울기(Gradient)를 계산할 수 있고 이 기울기에 방향을 따라서 이동을 한다면 maximize 또는 minimize 한 방향으로 state를 이동할 수 있게 됩니다. 이러한 아이디어가 Gradient method 가 되겠습니다. 이 방식은 굉장히 많이 사용되는 방식입니다. 딥러닝이라든지 여러 최고 알고리즘에서 최적화를 할 때 많이 사용되고 있습니다.

그렇다면 Gradient는 어떻게 구할 수 있을까요?
Gradient 는 벡터인데요. 만약 1차라면 미분해서 구하면 되고 n차, 즉 벡터 형태가 될려면 Gradient는 x1 에 대해서 미분, x2 에 대해서 미분,...., 즉 x 에 대해서 편미분을 구하고 이를 벡터로 구성하면 Gradient가 됩니다. 벡터이기 때문에 magnitude와 direction이 존재하는데 저희는 방향에 더 집중을 할 것입니다.이 방향이 결국은 목적함수에 가장 steepest slope로 나가는 방향을 나타내게 되고 그래서 저희는 Gradient만 구하고 그 방향으로만 state를 나아가면 되는 겁니다.
여기서 '얼마나 진행할 것이냐?' 라는 알파 Step Size 가 있습니다.

(maximize는 +, minimize - 입니다.) 위 과정을 반복하면 최대값/ 최소 값을 구할 수 있습니다.
당연히 스텝 사이즈도 잘 정해야합니다.
너무 작게 정하면 단계가 많아지고 반대로 너무 크게 정하면 Overshoot 이 일어나게 됩니다.

스텝 사이즈가 적당하면 검은색 그래프로 따라가게 되는데 스텝이 크면 빨간색 선처럼 큰 변동이 일어나는 것 입니다. 절대 미니멈 값에 도달할 수 없을 겁니다.
그리고 결론은 Gradient 값이 0이 되는 것을 찾는 겁니다. 이 때의 x 를 critical points 라고 합니다.
우리가 앞에서도 언급했던 'local minumum' 에 빠질 수 있는 가능성은 여전히 존재하긴 합니다. 하지만 좀 더 효율적으로 굳이 이웃을 계속 목적 함수로 계산할 필요 없이 기울기를 계산해서 방향을 바로 결정할 수 있다는 점에서 좋습니다.
많은 알고리즘에서 사용이 되고 딥러닝 부분에서도 많이 사용됩니다.
예시 : Gradient descent
mininum 을 구하는 거죠.



문제는 다음과 같습니다. 이를 보면 저희는 Continuous State Spaces 라는 것을 알 수 있습니다. 그럼 이를 미분하면 기울기를 구할 수 있습니다. 초기 값이 4고 step size 0.1 입니다. 그래프는 아래와 같습니다.

그럼 점점 아래의 그래프 방향처럼 점진적으로 minimum 에 도달하게 됩니다.

아래의 식처럼 진행되게 됩니다. Step 이 작으면 단계가 많아진다는 의미를 아시겠죠?

사실 저희는 기울기 2w 가 0이 되는 값, 2w = 0을 볼때 w = 0 을 도출해낼 수 있죠. 사실 이렇게 하는 게 가장 효율적입니다. 이렇게 구해지는 걸 'closed form' 입니다. 하지만 이렇게 구해지지 않을 가능성이 굉장히 높습니다.
Line Search 에 대해 가볍게 언급하고 지나가겠습니다. 이는 step size 알파를 가변화시키는 겁니다.
결국 기울기가 0이 되는 걸 구하는 거죠. 이 기울기를 g(x) 라는 함수라고 합니다. 이 함수의 해를 찾는거, finding roots 의 고전적인 방식인 Newton-Raphson method(1664,1690) 에 대해 알아봅시다. 마찬가지로 루트까지의 근사값을 점진적으로 찾아가는 겁니다.

파란색이라는 g(x) 함수가 있다고 가정합니다. 그럼 저희가 찾고자하는 것은 파란색 함수가 x 절편과 만나는 점을 찾아야합니다. 이를 x* 라고 합니다. 만약 xn 에서 시작을 한다고 할때 이를 미분하고 x 절편에서 만나는 점이 저희가 이동하게 될 xn+1 입니다. 이는 크게 점프를 한다는 걸 알 수 있죠? 그리고 g(xn+1) 을 넣은 곳에서 또 미분한 값이 x 절편과 만나는 곳이 xn+2 이고 또 이렇게 반복하는 거죠. 그러면 점점 해가 되는 값에 근접하게 됩니다. 이를 Newton-Raphson method 라고 합니다.



즉 저희는 Gredient 값이 0이 되는 값을 찾기 위해 이를 미분 시킨 값을 사용해야합니다. 이를 Hf(x) 라고 표현합시다. Hf(x) 는 g(x) 를 미분한 함수 입니다. 이를 Hessian matrix(이차 미분) 이라고 부릅니다.

조금 복잡할 수 있지만 이런 식으로 진행할 수 있다는 것도 알아두시면 좋습니다.

결국에는 위와 같은 식으로 표현이 가능할 것입니다. 하지만 사실 이렇게 미분을 계속 진행하는 것이 쉬운 상황이 아닙니다. 그래서 많이 사용하지는 않습니다. (Hessian 은 n^2 의 엔트리를 가지고 inverted 도 해야하기 때문에 복잡합니다.) 참고하시면 되겠습니다.
Constrained Optimization Problem
그럼 이제 Constrained Optimization Problem 에 대해 알아보겠습니다. 이는 앞에서 했던 Continuous state spaces 에 제한 사항이 생기는 겁니다. 예를 들어서 아래와 같은 식이 있다고 생각을 해 봅시다.
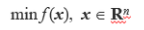
minimize 로 통일을 하고 생각을 해봅시다. 위 식이 이때까지 저희가 배운 겁니다. 하지만 이제 다음과 같은 제약이 생기는 겁니다.

위와 같이 g(x), h(x), x 의 범위에 제한을 두는 것을 Constrained Optimization Problem 이라고 합니다.
Ll 와 Ul로 x의 범위를 제한 함으로써 Search space S 가 정의됩니다. 위에 식에서 x 는 실수 전체 범위였습니다.
그리고 앞에서 주어진 q(equality constraints) 와 k-q (equality constraints) 가 feasible region F(S에 부분) 을 정의합니다. 이 제한 되어 작아진 feasible region 안에서 solution을 찾아야하는 겁니다.
다른 방식으로 공식화를 해봅시다. Penalty Method 라는 것이 있습니다. 이는 만약 제한 조건을 지키지 않을 시에 발생하는 감점 제도 같은 겁니다. 아래와 같이 벌점 함수인 vj(x) 를 정의할 수 있는거죠.
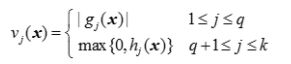
gredient 에 제한을 줬는데 이게 지켜지지 않는다? 그럼 그 값 만큼 페널티를 주는 겁니다. 작으면 작은만큼 크면 큰만큼 페널티겠죠. 아래도 hj(x)가 0보다 크면 안되는데 컸을 때 큰 만큼 페널티를 주는 겁니다. 이에 대해 weight 를 부여하면 다음과 같이 되겠죠. 이 가중치는 또 하기 나름이겠죠?
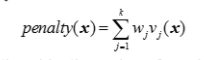
즉 다음과 같은 새로운 목적함수를 만들게 됩니다. 즉 이 프라임 에프를 최소화하는 것이 에프 엑스를 최소화 하는 방법이라고 할 수 있습니다. 이 새로운 목적함수는 제한이 없는겁니다. penalty(x) 라는 함수를 통해 제한을 없애 버렸기 때문이죠. 즉 COP 가 unconstrained optimization problem 으로 바꿔준 겁니다. 사실 이렇게 페널티를 둔다는 것이 최적화를 보장해주진 않습니다. penalty가 0이 된다는 보장이 없기 때문이죠.

이제 이 penalty 가 0이 되게 보장하는 방식이 KKT(Karush-kuhn-Tucker) 입니다. 이는 좀 복잡하기 때문에 다음 게시물에서 이이기를 해보겠습니다.
'공부 > 인공지능' 카테고리의 다른 글
| [인공지능] 7.Knowlege Representation (0) | 2020.10.15 |
|---|---|
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |
| [인공지능] 4.Local Search Algorithms (0) | 2020.10.13 |
| [인공지능] 3. Informed Search (0) | 2020.10.07 |
| [인공지능] 2.Uninformed Search(Blind Search) (2) | 2020.09.28 |



