Bayesian Networks
- The Syntax of Bayesian Networks
- The Semantics of Bayesian Networks
- Constructing Bayesian Networks
- Conditional Independence Relations in Bayesian Networks
- Compact Conditional Distributions
- Hybrid(discrete + continuous) Networks
- Continuous Child Variable
- Discrete Variable with Continuous Parents
Conditional Independence Relations in Bayesian Networks
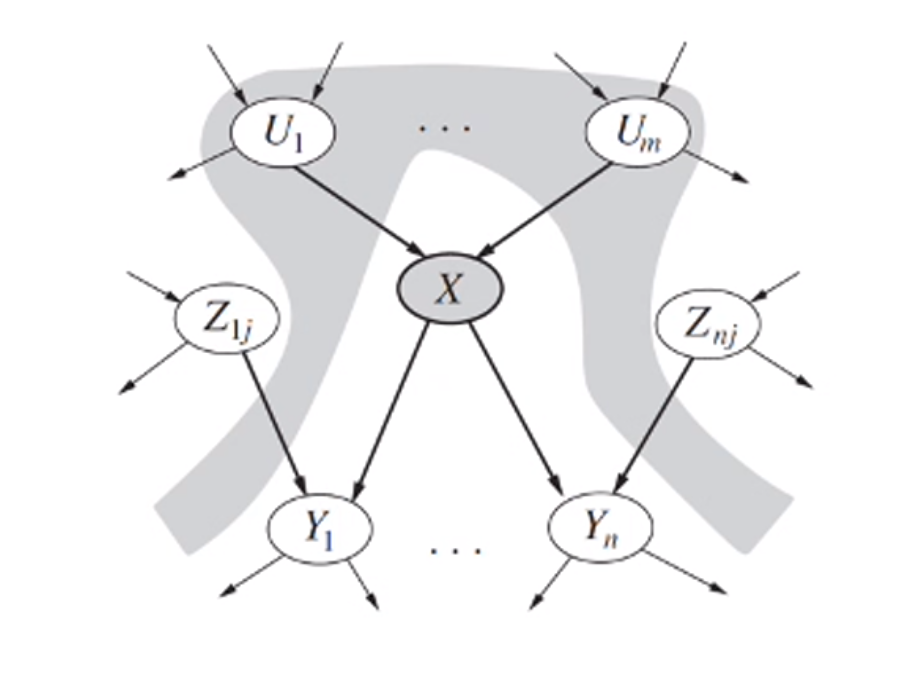
노드 X의 parent 노드는 U1~Um 까지 총 m 개가 있습니다. 자식 노드는 Y1~ Yn 까지 총 n 개가 존재합니다. 그리고 이 Y1 은 child 가 있을거고 각각 다 child 가 있겠죠? 이렇게 확장성이 있는데 이렇게 자식 노드로 쭉쭉 나아가는 게 X의 descendants 라고 하는 겁니다. 하지만 Z 노드 라인은 X와 직접적인 연결이 없기 때문에 descendants 라고 할 수 없습니다. 그래서 위 회색 영역은 Topological(위상수학) 하게 X의 자식 노드가 아닌 부분을 영역화 한 겁니다. 여기서 얘기하고 싶은 건
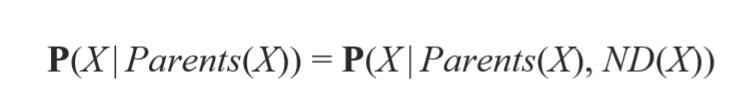
이 수식은 Parnets가 주어졌을 때 노드 X의 distributions 을 이야기 하는 겁니다. 즉 ND(X), Non-Descendants 에 대한 내용이 주어지더래도 영향을 미치지 못한다. 라는 말입니다. 즉 Conditionally independent 하다. Z 와 같은 상관없는 노드가 와도 영향을 끼치지 못한다는 의미입니다.
간단한 예제를 보면서 앞에서 이야기한 부분을 살펴봅시다.
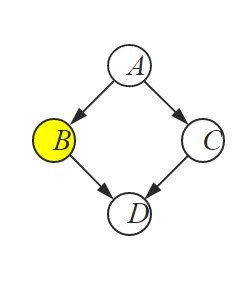
a 가 참, c 가 참이라는 조건이 주어졌을때 distributions을 계산을 하는 문제로 생각을 해봅시다. 먼저 노드 B와 다른 노드의 관계를 확인할 수 있습니다. 여기서 노드 C 가 non-descendants 이라는 것을 알 수 있습니다. 독립적인 환경이 되는 거죠. 계산을 쭉 해보면 2번째 항처럼 풀어낼 수 있습니다. 베이시안 네트워크를 사용하기 위해서는 모든 노드가 나와야함으로 d 를 추가해줍니다.
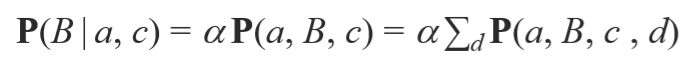
이 뒤로는 저번 시간에 배웠던 각 노드에 부모 값을 사용해서 계산을 해줍니다.

노드 A 는 부모가 없기 때문에 P(a)
노드 B 는 부모가 있기 때문에 a
노드 D 는 부모가 두 개기 때문에 둘 다 P(d|B,c) 입니다.
보시면 d 가 있는 항에만 시그마가 영향을 미치기 때문에 나머지 항은 다 앞으로 빼낼 수가 있습니다.
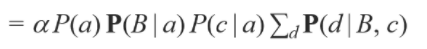
여기서 d 에 조건이 주어지긴 했지만 모든 값에 대한 합은 당연히 1 이 될 겁니다. 만약 d가 c 의 위치에 있었다면 합이 1이 되진 않았을 겁니다. 앞에 있을 때는 확률의 합이 다 1이 될 것 입니다. 그래서 시그마 부분을 날라가게 됩니다.
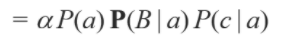
그리고 가운데 항을 제외한 나머지 두 항은 값으로 주어질 거기 때문에 다음과 같은 표현이 가능합니다.
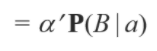
여기서 알파 프라임을 날리면 결과적으로는 다음과 같아집니다.
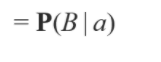
최종적으로 c 의 영향이 사라지는 것을 볼 수 있습니다. 즉 Conditional Independence 하다는 것을 알 수 있습니다. 전체적인 과정은 다음과 같습니다.
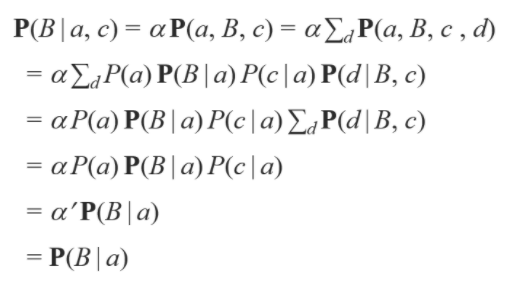
다음은 자손을 추가한 경우입니다.
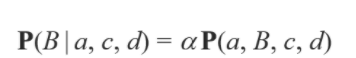
마찬가지로 normalization을 할 수 있고요. 마찬가지로 베이시안 네트워크로 다음과 같이 표현이 가능합니다.
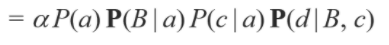
여기서 P(a) 와 P(c|a)는 값이기 때문에 위에서와 같이 새로운 알파 프레임으로 표현을 해줍니다.
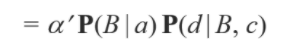
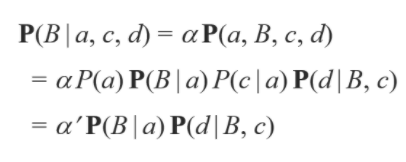
즉 d 가 주어졌을 때는 Conditional Independent 하지 않다는 것을 알 수 있습니다.
이번에는 또 다른 topology 로 컨디셔널 인디팬던트 이야기를 해보겠습니다.
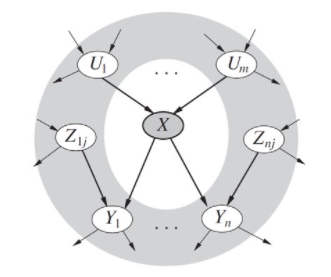
이 X노드도 똑같이 U 부모, Y 자식 노드가 있죠. 위에서는 관계가 없었던 Z 노드, 이를 포함시키는 Markov blanket 입니다. 이 마코브 블랭킷이 주어지면 이를 영역을 제외한 모든 다른 노드는 independent 하다는 겁니다.

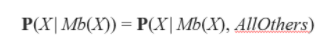
회색 띠 = Mb(X)
마코브 블랭킷을 나타냅니다.
추가적으로 다른 어떤 노드가 주어져도 컨디셔널리 독립적이다라는 거죠. 예시로 확인해볼까요?
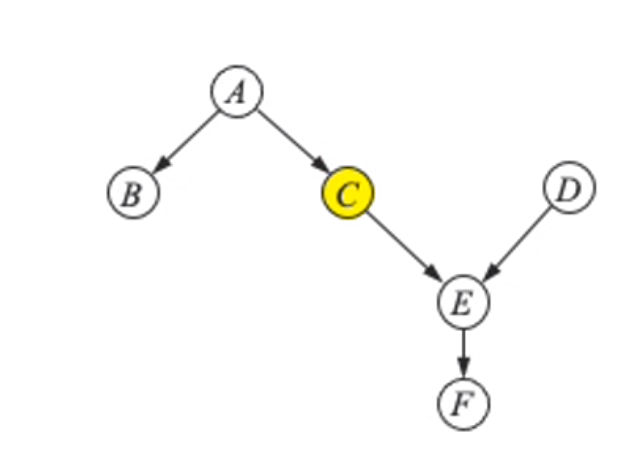
그래프에서 노드 C의 distribution을 구해봅시다.
앞에서와 똑같은 순서로 진행하면 됩니다.
1. 관계 살펴보기
A는 C의 부모, E는 자식, D는 자식의 부모입니다. 그리고 B,D가 All others 에 속합니다.
여기서 마코브 블랭킷은 A,E,D 입니다.
2. 조건부 독립 사용하기

여기서 B,D 는 수식에 전혀 영향을 끼치지 못한다고 이야기할 수 있습니다.
3. 계산하기
3-1) 컨디션 풀어내기
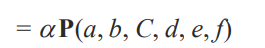
이때 모든 노드가 나와있지 않을 경우에 베이시안 네트워크 사용
3-2) 부모 노드에 관계에 따라 전개
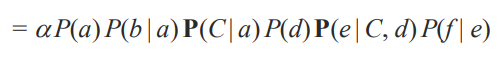
3-3) 값에 해당하는 건 알파 프라임으로 묶어버리기
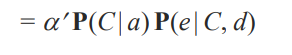
C에 관한 distribution 이 두개가 남았네요.
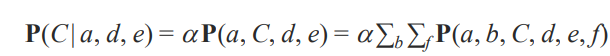
Markvo Blanket 에 있는 것만 사용해서 계산해봅시다. 위와 같은 결과가 나오는지를 확인하고 싶은 거죠.
마찬가지로 컨디션을 풀어내고 모든 노드를 넣기위해 시그마를 넣고 그리고 위해서 했던 부분을 반복하는 겁니다.
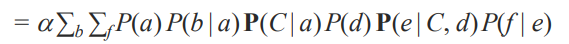
시그마가 영향을 끼치는 부분만 확인해줍니다.
즉 B,F 와 연관없는 부분은 앞으로 빼줍니다.
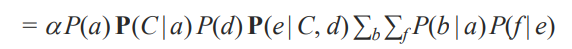
그리고 각각 관련있는 시그마로 빼줍니다.
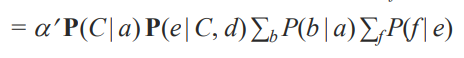
이런 시그마는 컨디션이 아니면 다 합이 1이 됩니다.
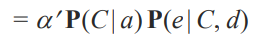
최종적인 값입니다.
이는 위에서 했던 것과 동일한 값이죠. 즉 Conditional Independence 하다는 것을 알 수 있습니다.
전체

Compact Conditional Distributions
베이시안 네트워크 중 가장 큰 장점은 초반에 배웠던 full joint distribution에 비해서 엔트리 수를 급격하게 줄일 수 있다는 장점이 있었습니다. 그런 베이시안 네트워크 내에서도 엔트리 수가 증가하는 경우가 있습니다. 어떤 부모가 있으면 폴리노미얼이 아니라 익스포넨셜하게 늘어나게 됩니다. 이게 내부적으로 있는 문제점이죠. 그래서 제시되는 솔루션이 Noisy-OR distributions 입니다. 몇가지 가정을 해보겠습니다.
- K 개의 부모가 존재, 모든 cause 를 포함한다.
- Negated causes ㄱUi 는 X에 영향을 미치지 않는다.
- 각각의 cause 가 단독으로 Independent failure probability qi 을 가지고 있다.
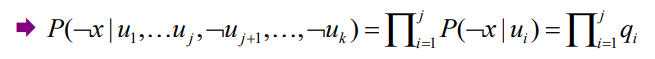
이 파트는 이해하기가 좀 힘들었는데 예제를 보면서 확인을 해봅시다.

보시면 Cold,Flu,Malaria 라는 Parents 가 있고 Fever 라는 현재 노드가 있습니다. 이에 관한 CBT 를 나타낸 것이죠. 지금은 부모가 3 이기 때문에 2^3 =8 개의 경우가 나옵니다. 하지만 이게 많아지면 굉장히 부담스럽게 테이블이 커지게 되겠죠. 이를 redution하는 법을 배워보는 것입니다. 여기서 핵심이 되는것이 Independent failure probability입니다. 즉 각각의 원인이 단독으로 발생을 했을 때 Independent failure probability가 존재를 한다는 겁니다. 다시 말해서 아래의 그림과 같이 단독 True 일 경우 Fever 가 False 일 값이 주어진다는 겁니다. 즉 0.1,0.2,0.6 이 주어졌을 때 우리가 나머지 엔트리에 대해서도 다 계산을 할 수 있다는 겁니다. 그것이 failure probability 에서 Independent 하다는 겁니다.

'공부 > 인공지능' 카테고리의 다른 글
| [머신러닝 과제] 로지스틱 회귀와 k-NN 구현 (0) | 2021.05.11 |
|---|---|
| [인공지능] 9.Bayesian Networks (0) | 2020.10.16 |
| [인공지능] 8.Uncertainty (0) | 2020.10.15 |
| [인공지능] 7.Knowlege Representation (0) | 2020.10.15 |
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |



