Bayesian Networks
저희가 저번 강의에서 공부한 Conditional independeant 의 연장선이라고 생각하시면 됩니다. 목차는 다음과 같습니다.
- The Syntax of Bayesian Networks
- The Semantics of Bayesian Networks
- Constructing Bayesian Networks
- Conditional Independence Relations in Bayesian Networks
- Compact Conditional Distributions
- Hybrid(discrete + continuous) Networks
- Continuous Child Variable
- Discrete Variable with Continuous Parents
The Syntax of Bayesian Networks
예시를 보면서 베이시안 네트워크(Bayesian Networks) 에 대해 알아봅시다.

Weather 는 discrete variable 이고 sunny, rain, snow, cloud 이렇게 네개의 값을 가지고 있었습니다. 그리고 치과에 관련된 세 개의 변수도 보이네요. 이들은 boolean variable 입니다. 그리고 치과 관련 변수와 날씨는 독립적입니다.
또 중요한게 Toothache 와 Catch 는 Cavity 가 주어지게 되면 독립이 되는 conditional independent 관계입니다. 이런 관계도를 화살표를 통해서 만들 수 있습니다.
그러면 이렇게 세 개의 변수가 주어졌을 때 Probability 를 계산을 해보겠습니다.
chain rule 을 통해 확률의 곱으로 계산을 할 수 있습니다.
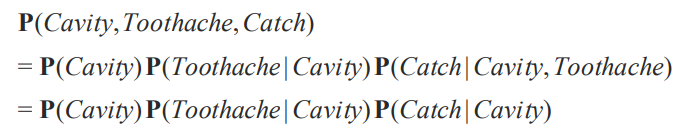
이런 simple, graphical notation을 Bayesian Networks 라고 합니다. 이를 통해 variable 들 간에 관계나 독립이나 확인을 할 수가 있겠죠. 이런 확인된 독립 관계를 통해서 compact specification of full joint distributions 을 구할 수 있습니다. 애초에 독립이 full joint distributions 을 현실적으로 쓰기 위해 나온 방안이니깐요.
베이시안 네트워크도 그래프니깐 노드와 엣지로 구성을 할 수 있을 겁니다.
원인과 결과, 즉 방향이 있으면 directed
그리고 사이클이 생기는 상황을 고려하지 않기 때문에 acyclic graph 입니다.
이러한 베이시안 네트워크 그래프를 통해서 conditional distribution 을 각각의 노드에 대해서 계산할 수 있습니다.
그 때 컨디션으로 주어지는 것이 결국에는 그 노드의 부모 노드에 대해 컨디션이 주어지면 그 노드의 conditional distribution을 구할 수 있을 겁니다.
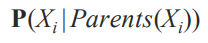
가장 간단한 경우는 이 conditional distribution이 테이블 형태로 나타나는 CPT 로 나타나는 겁니다.
예제를 통해 베이시안 네트워크를 구성해봅시다.

변수는 다음과 같이 구성이 될 겁니다.
statement 을 한번 써봅시다.


원인과 결과를 통해 그래프를 쓸 수 있습니다. 여기에 CPT 를 추가해줍시다. 그러면 Bayesian Networks 가 되는 겁니다.
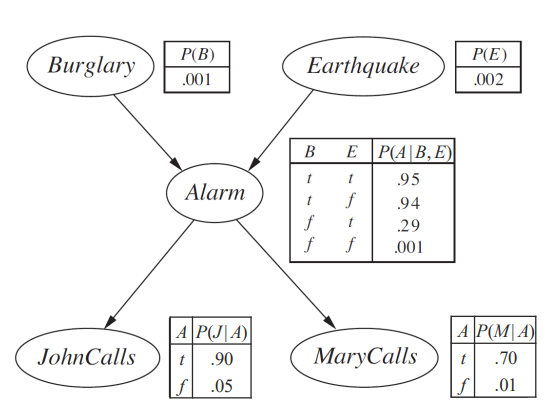
주의할 점은 Condition들의 조합의 합이 1이 되지 않는다는 겁니다.
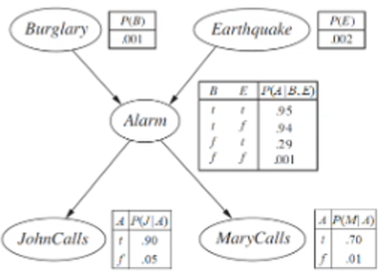
Compactness
각 노드에 대해서 CPT 를 제공을 해야합니다. 만약 k 의 부모가 있으면 2^의 조합에 대해서 probability 를 계산해야합니다. 각각의 variable 가 최대 k 개의 부모를 가지고 있다면 O(n2^k) 입니다. Bayesian Networks 를 써서 복잡도를 줄일 수 있습니다. linear 하게 변하게 됩니다. 여기서 burglary net 을 계산해보면 B,E 는 1, A 는 두 개의 부모가 있으니 4개, J,M 은 하나의 부모가 있으니 2개입니다. 총 10개가 되죠. 하지만 이를 full joint distribution으로 변환하면 2^5 - 1 = 31 입니다.
Bayesian Network의 Semantics를 Numerical 한 관점해서 이야기 해봅시다. 이는 full joint distribution을 local conditional distributions 의 곱으로 정의됩니다. 각각 노드를 부모 노드로 확률을 계산한 겁니다. 저희가 full joint distribution으로 계산을 할 수 있었지만 이는 현실적으로 불가능하다고 언급하였습니다. 결국은 conditional distributions 을 통해서 entry reduction (이 접근을 Bayesian Networks 로 하는 겁니다.) 한 겁니다.
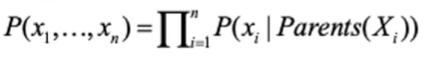
먼저 각각의 변수를 구하고 정의를 하고 변수들 간에 관계도를 그리게 되면 그래프 각각의 노드에 대해 CPT를 제공하고 이를 기반으로 query 에 대한 확률을 계산할 수 있습니다. 결국은 앞서서 본 체인 룰로 풀어낼 수가 있었습니다. 그러고 conditional independence 를 이용해서 reduction 하게 되었는데 결국은 같은 결과가 나옵니다. 그러니 이게 Bayesian Network를 이용하는 것과 동일하다는 점, 그런 큰 그림을 이해하는 것이 좋습니다.

첫 번째 줄은 chain rule 로 나타내고 베이시안 네트워크를 통해 정리한 겁니다. 보면 부모노드로 정리되는 것을 볼 수 있습니다. 처음에 본 공식과 똑같다고 보면 됩니다.
예시를 한 번 보겠습니다. 다음과 같은 문제가 있습니다.
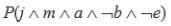

이렇게 베이시안 네트워크를 구하고 이걸 통해 모든 변수들의 확률을 직접적으로 구할 수 있습니다. 결국은 이러한 네트워크를 어떻게 구성하는지가 관점이 되겠습니다.
Construction Bayesian Networks
변수 정의하기
-boolean인지 discrete 인지
1. X1...,Xn 까지 ordering 하기
중요한 시작점입니다. 순서에 있어 적절하지 않으면 복잡해지기 때문입니다.
간단한 동작은 원인이 먼저 나오고 결과가 나오는 겁니다. 가장 적절한 순서라고 볼 수 있습니다.
2. For i = 1 to n
각각의 순서대로 Xi 를 네트워크에 추가합니다.
여기서 P(Xi|Parents(Xi) 를 구할 때 앞에 있는 노드들을 고려를 해주어야합니다. 여기서 Parents(Xi) 만 되는 노드를 선택하게 됩니다. (X1~Xi-1 까지) 아래 그림과 식을 함께 보시면 이해가 되실 겁니다.
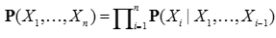
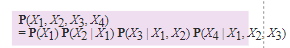
X3를 확인해 볼까요? 여기선 X3 의 부모로 X1, X2 가 적혀져있는게 이 모든게 부모 노드이냐? 그것은 결국 변수 간의 관계에 달려있습니다. 안될 수도 있습니다. 이 단계는 즉 Xi 와 이 부모를 정의하는거라고 생각하시면 됩니다. 결국 이 부모의 선택이 이 numerical semantics 를 보장합니다.
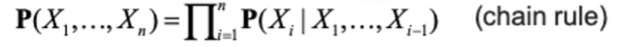
따라서 다음과 같은 chain rule로 확률을 구할 수 있습니다.
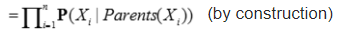
다음과 같이 구성을 하는 거죠. 부모만 연결될 수 있는 걸 선택을 해서 컨디션으로 주어지게 되는 겁니다. 즉 체인 룰로 나타낸 위의 식이 full joint distributions 인 것을 알 수 있죠. conditional independence 를 이용해서 부모만 선택하기 때문에 entry reduction 효과를 볼 수 있는 겁니다.
예제를 살펴봅시다.

앞서 했던 순서는 E,B,A,J,M 이었죠. 이는 원인 뒤에 결과가 나오는 순이었습니다. 이번 예제는 반대로 나오게 구성을 했을 때 얼마 Bayesian Networks가 복잡해지는지 알아보는겁니다.

처음으로 M이 들어갔을 때는 부모가 없으니 아무것도 없겠죠. 그러다 J가 들어갔습니다. M이 있으니 이를 통해 independence 를 해봅시다. 지금 이에 대해 아무런 정보가 없습니다. 즉 존이 전화를 했는데 메리가 전화를 했는지 안 했는지 정보를 알고 있을 때, 즉 알람이 울렸다고 생각하고 메리가 전화를 했다는 것을 존이 알고 있다면 존도 영향을 받습니다. 여태 배웠던 상황과는 다르다는 것을 알 수 있죠.지금은 말 그대로 아마 메리가 전화를 하는게 존이 전화를 하는데에 영향을 미치겠죠?

여기 NO 라고 적힌거는 관계가 있다는 , 즉 독립적이지 않다는 의미입니다. 이번에는 Alarm 이 추가가 되었습니다. 그럼 JM에 대해서 어떠한 관계가 있을까요? 뭐랑 독립적인지에 대한 관계들을 다 따져보아야합니다. 그랬을 때 알림의 경우는 두 가지 다에 영향을 받을 수 밖에 없을 겁니다. 이는 독립적이지 않다는 의미이죠.
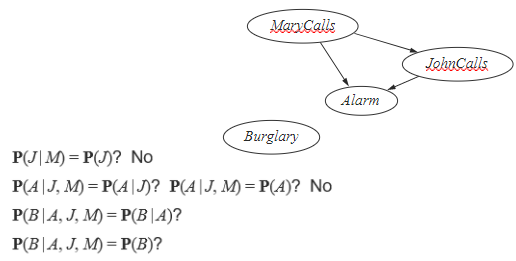
Burglary 는 Alarm 에만 영향을 받습니다. 다음과 같이 쓸 수 있겠죠.

이제 마지막으로 Earthquake를 추가해봅시다. conditional 한지 확인해 봅니다. 그럼 최종적으로 burglary와 alarm 이 영향을 받는다는 것을 알 수 있습니다.
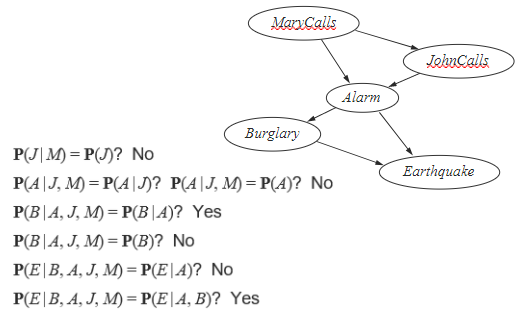
이처럼 결과를 생각하고 원인을 보는 것이 저희의 자연스러운 논리흐름에는 방해가 된다는 것을 알 수 있습니다. 어쨌든 꾸역꾸역 구성을 해냈네요. 논리흐름대로 진행을 했을 때는 4개로 끝났는데 여기선 엣지가 6개네요. 커넥션이 늘어나면 복잡도가 늘어나는거죠. 아래를 보면 더 복잡한 걸 알 수 있습니다. 그전에는 10개 였는데 여기서는 13개의 숫자가 필요하네요.
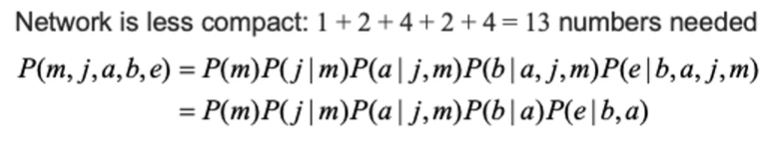
그럼 오늘은 이만 여기서 마치겠습니다! 잘 보셨다면 좋아요와 구독, 광고도 눌러주시면 감사하겠습니다.
'공부 > 인공지능' 카테고리의 다른 글
| [머신러닝 과제] 로지스틱 회귀와 k-NN 구현 (0) | 2021.05.11 |
|---|---|
| [인공지능]10.Bayesian Networks 2 (1) | 2020.12.07 |
| [인공지능] 8.Uncertainty (0) | 2020.10.15 |
| [인공지능] 7.Knowlege Representation (0) | 2020.10.15 |
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |



