Uninformed Search는 Blind search 라고 합니다.
이는 '현재 상태에서 목표 상태까지 Step의 갯수(Path Cost)를 모른다' 라는 의미힙니다.
Informed(Heuristic)라고 하면 어떤 상태가 목표 상태로 가는데 적합한지를 아는 것을 의미합니다.
여행 가서 길을 찾는 것과 고향에서 길을 찾는 것이라 생각할 수 있겠네요.
여행을 가면 그냥 앱을 따라가지만 고향에서 길을 찾으면 어떤 버스가 더 빠른지 어디서 환승하는 게 더 나은 지 생각 할 수 있잖아요.
Uninformed Search는 6가지가 있습니다.
1. Breath-First Search(너비 우선 탐색)
2. Uniform-Cost Search(일정 비용 탐색)
3. Depth-First Search(깊이 우선 탐색)
4. Depth-Limited Search(깊이 제한 탐색)
5. Iterative Deepening Search(점차적 깊이 제한 탐색)
6. Bidirectional Search(양방향 탐색)
위 6가지 종류의 Uninformed Search는 H(n) 을 계산하지 않는 겁니다.
H(n) 는 현재 상태에서 목표상태까지 얼마나 남았는지를 보여주는 함수입니다.
Blind Search 는 이를 알 수 없는거죠.
그러니 당연하게도 최적 해를 구하기는 좀 어렵다고 볼 수 있습니다.
이제 하나씩 확인해봅시다.
그 전에 다음 변수 의미를 알고 들어갑시다.
b : Branching Factor 혹은 전체 자식 Node 의 최대 갯수를 의미합니다.
d : 가장 얕은 Goal Node 의 깊이를 의미합니다.
m : 상태 공간에서 가장 길이가 긴 경로를 의미합니다. (주로 양의 무한)
1. Breadth-first Search
Frontier 에서 가장 얕은 방문하지 않은 노드를 먼저 확장하는 방법입니다.
여기서 Frontier 은 FIFO Queue 로 구현 되어야합니다. GRAPH-SEARCH 을 기반으로 구현합니다.
TREE-SEARCH 기반으로 구현할 수도 있지만 효율적이지 못하죠.

A가 Frontier 에 들어가고 A가 빠지면 A의 자식노드인 B,C 가 큐로 들어오고 알파벳 순에 따라 B가 빠지면 B의 자신 D E 가 Frontier 에 들어가고 C가 빠지고 F, G 가 들어옵니다.
BFS는 Frontier 에 넣기 전에 Goal test 를 합니다.
-Evaluation
Complete : O
Optimal : O
Time & Space Complexity : 1 + b + b ^ 2 + b ^ 3 + ... + b ^ d = O(b ^ d)
복잡도는 가지를 뻗을 때 마다 두개씩 자식 노드가 생기고 내려오기 때문입니다.
Uninformed Search이기 때문에 길에 대한 정보가 없으므로 모든 Node 다 뒤져봐야하기 때문입니다.
이는 최악의 복잡도인데요.
만약 G 가 아니라 B 가 Goal State 면 다른 복잡도가 나오겠죠?
또 만약 해당 노드를 확장한 다음, 즉 Frontier 에 넣고 나서 Goal Test 를 하면 복잡도는 O(b ^ ( d+1 ) ) 이 될겁니다.
BFS 에 단점은 메모리 요구량이 크다는 건데요. Blind Search 는 이 문제를 해결하지 못합니다.
동일한 이야기로 최적화시키는 길에 대한 정보가 없기 때문입니다.
이 단점을 극복하기 위해 Frontiner 에 크기 제한을 둔 Beam Search가 있습니다. 이건 informed search 입니다.

2. Uniform-Cost Search
Uniform-Cost Search 는 현재 Frontier 에서 확장되지 않은 노드 (=방문하지 않은 노드) 중에 가장 비용이 적은(=거리가 가까운) 노드부터 선택하여 확장합니다.
여기서는 Priority Queue 로 구현이 되어야합니다. 비용에 따라 정렬되는 Priority Queue 입니다.
가장 낮은 비용을 가진 노드가 Queue 에 가장 앞에 놓이게 된다는 거죠.
비용이 높은 노드는 끝까지 못 나갈 수 있다는 의미이죠.

그림 b 를 보면 비용이 11인 A 밑에 G는 비용이 10인 B 밑에 G 가 나오면 대체됩니다.
결과적으로 이 Uniform-Cost Search 는 깊이나(DFS) 너비(BFS) 에 따라서 탐색하는 것이 아닌 오직 현재 상태에서 가장 비용이 적은 노드로 이동하는 것 입니다. 즉 가장 짧은 거리를 추측하는 평가함수인 H(n) 이 0인걸 알 수 있지요. 이 알고리즘의 단점이라면 무한 루프에 빠질 수 있다는 겁니다.
-Evaluation
Complete : O
Optimal : O
Time & Space Complexity : O(b^(1+[C*/c]))
C*는 최적 해의 비용입니다
이 알고리즘은 보통 BFS 보다 효율적입니다.
만약 step cost 가 다 같으면 b^[1+d] 가 될겁니다.

3. Depth-First Search(DFS)
깊이 우선 탐색 방법입니다.
Frontier 에서 확장되지 않은 노드 중에서 가장 깊은 거 부터 확장되는 방식인데요.
BFS 가 Queue이라면 DFS 는 Stack 형태로 구성됩니다.
Tree-Search-Based 측면에서 이 DFS에서도 무한 루프를 피하기 위해 새로운 State 가 나올 때마다 선조 노드를 확인해서 중복이 있으면 바로 새로운 State 를 폐기처분 하는 겁니다. 그렇기 때문에 메모리 요구량은 보통 정도입니다.
Graph-Search-Based 라고 해도 Explored Set은 지수적 Memory 양을 가져야 하기 때문에 별로 의미가 없습니다.
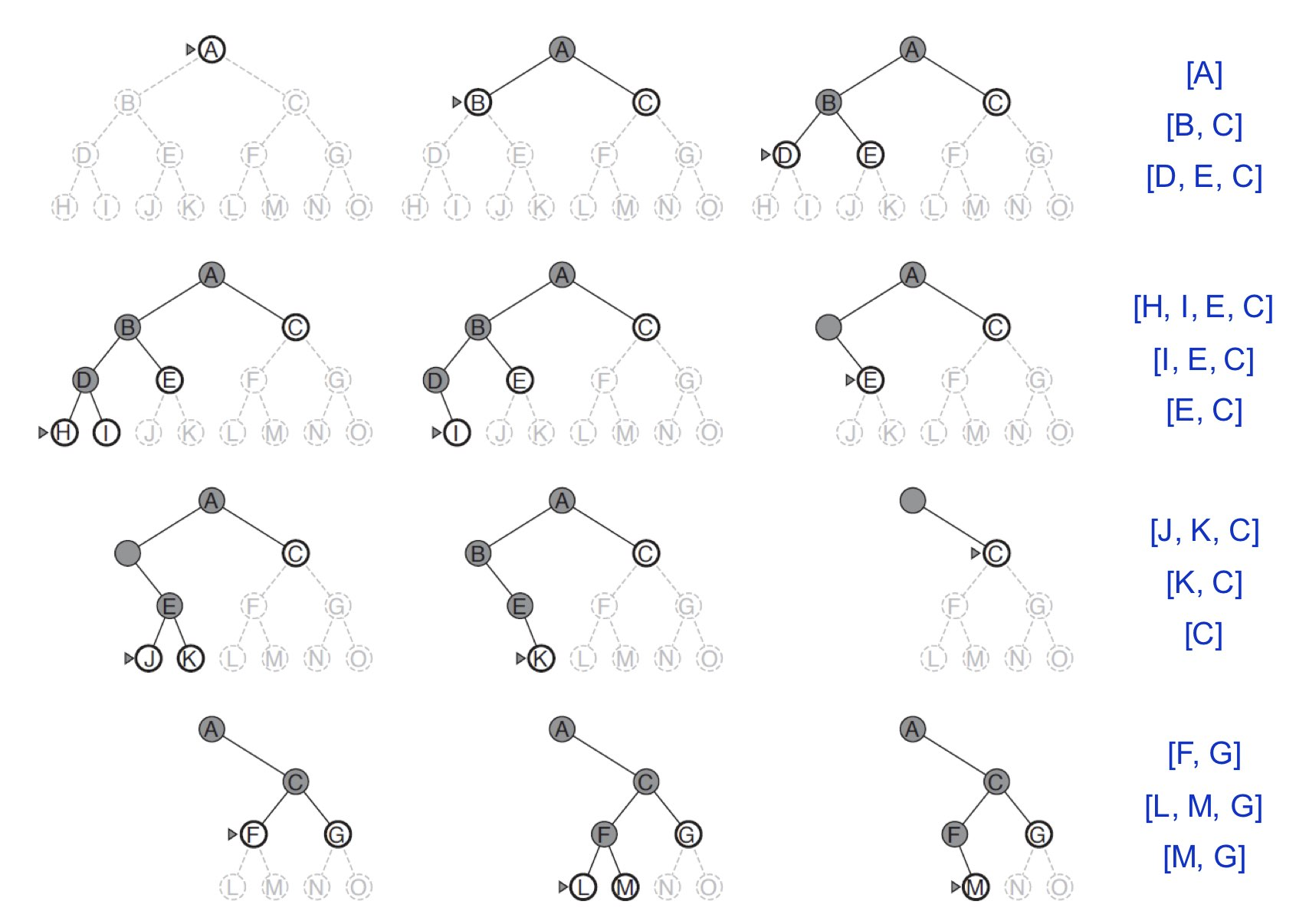
-Evaluation
Complete : No
Optimal : No
Time : O(b^m)
Space Complexity : O(bm)
만약 m이 d 보다 훨씬 크다면 치명적인 알고리즘입니다.
그 이유는 BFS 로 했다면 금방 찾을 깊인데 (예를 들면 C,F,G) DFS는 한 노드만 죽어라 파는 형식이기 때문에 멀리 돌아오게 되는 거죠.
m : 상태 공간에서 가장 깊은 Depth
d : Goal 노드 중에서 가장 얕은 Depth
보통 BFS 보다 훨씬 빠른 경향이 있습니다. 하지만 끝없이 깊은 경로로 들어가면 영원히 해를 찾지 못하고 Search 가 끝나지 않을 수도 있습니다.
Complete 하지도 않고 Optimal 하지도 않습니다.
만약 유한하면 Complete 할 수도 있습니다.
하지만 운이 미친듯이 좋지 않은 이상 불필요한 경로 탐색은 늘 존재하기 때문에 Optimal 하지는 않습니다.
4. Depth-Limited Search
DFS 와 거의 일치하지만 차이는 깊이 제한을 둔다는 점이 있습니다. 깊이 제한 L 을 두고 이 이상으로는 탐색을 하지 못하는거죠. 일반적으로 Tree-Search-Based 의 경우에 사용됩니다.
-Evaluation
L이 d 보다 크지 않으면 Complete,Optimal 둘 다 하지 않습니다.
Time : O(b^L)
Space Complexity : O(bL)


5. Iterative Deepening Search
DLS에서 Limit를 점점 늘려나가는 방식입니다.
전체 지름을 알지 못한다면 좋은 방법입니다. (점진적으로 진행할 수 있기 때문에)
Graph-Search-Based 방식은 별로 의미가 없습니다. 매우 많은 메모리를 요구하기 때문이죠.
심지어 메모리 요구량이 많은 BFS 보다도 많습니다.
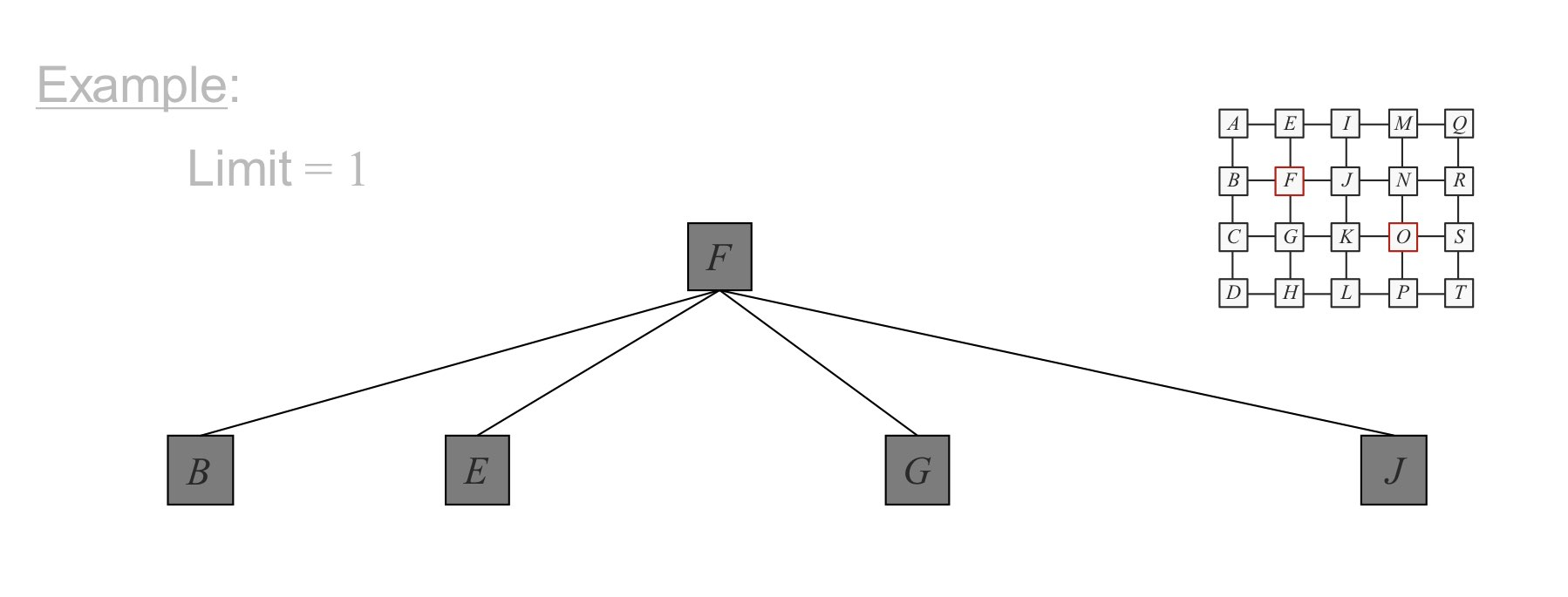

이렇게 Limit 를 하나하나 늘려나가는 겁니다.
-Evaluation
Complete : O
Optimal : O
Time : O(b^d)
Space Complexity : O(bd)
이게 Depth-Limited 보다 훨씬 별로라는 생각이 들 수도 있지만 b=10 이고 d =5 라면 Depth-Limited 는 111,110이고 Iterative-Deepening 은 123,540 으로 차이가 크게 나지 않습니다.

6. Bidirectional Search
시작 노드와 끝노드에서 동시에 탐색을 시작하는 겁니다. 이렇게 하는 이유는 BFS 에 비해 시간과 공간을 줄일 수 있기 때문입니다.
이 방식은 검색시간을 엄청 빠르게 줄일 수 있지만 항상 사용가능하진 않습니다.

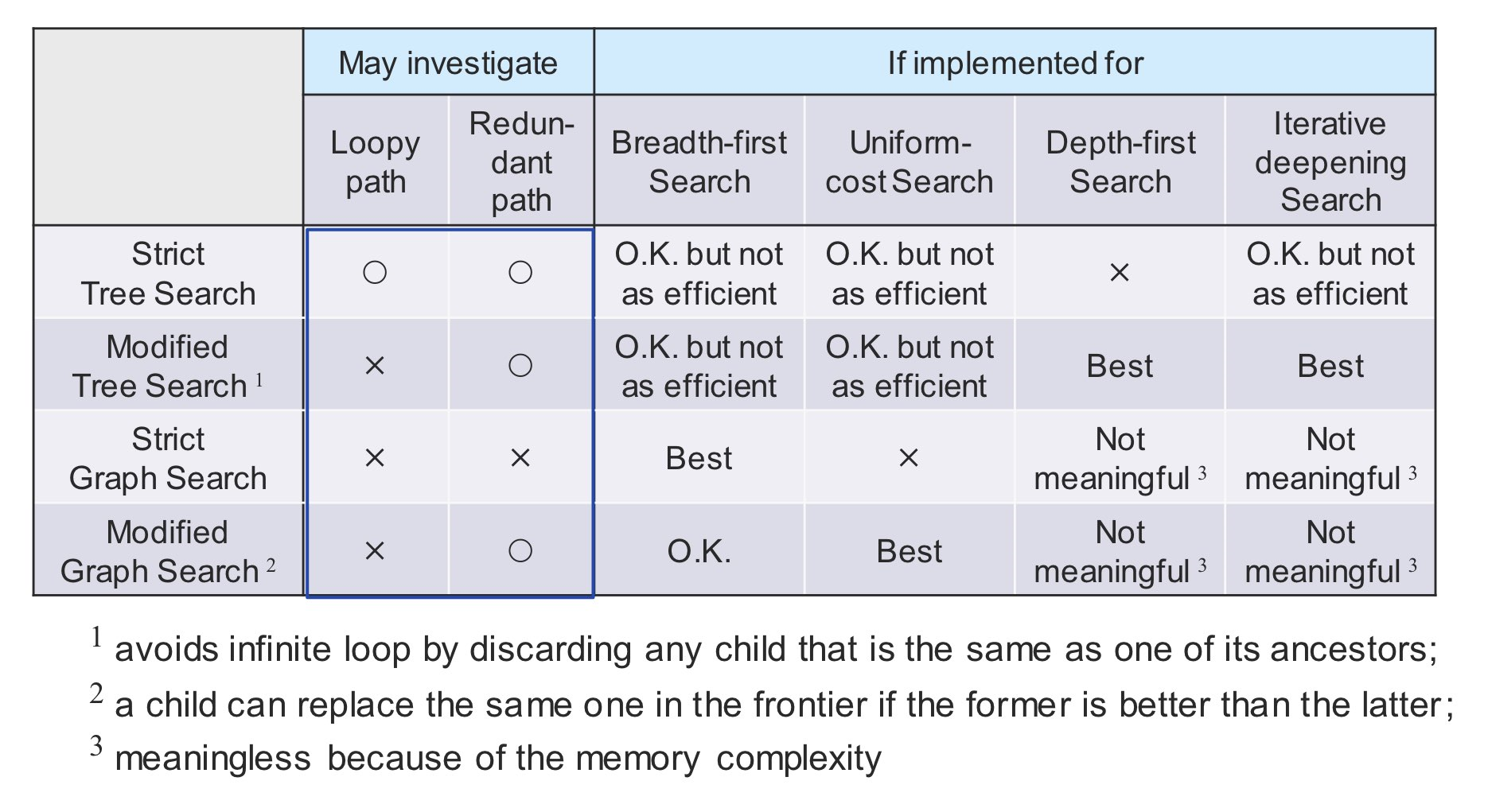
트리 기반 그래프는 각 노드에 부모 노드 정보를 통해 역추적을 하여 loopy path 여부를 체크합니다.
Strict Tree Search 는 이런 loopy path 여부를 체크하지 않습니다. Modified 에서 이 과정이 추가 됩니다.
Graph Search는 explored set 이 있어서 이를 통해 loopy, redundant path 모두 체크하고, modified 에서는 redundant 를 일부 허용 하는 겁니다.
'공부 > 인공지능' 카테고리의 다른 글
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |
|---|---|
| [인공지능] 5.Continuous State Spaces & Constrained Optimization Problem (0) | 2020.10.14 |
| [인공지능] 4.Local Search Algorithms (0) | 2020.10.13 |
| [인공지능] 3. Informed Search (0) | 2020.10.07 |
| [인공지능] 1.인공지능 기초 용어 정리 (0) | 2020.09.28 |



