Informed Search(=Heuristic Search)는 노드가 가장 전도유망한 방향으로 탐색되는 것을 말합니다.
Uninformed Search(=Blind Search)에서는 경험적으로 분석을 할 수 없기 때문에 Goal State 로 탐색이 진행될 때 각 Search 들 만의 규칙을 가지고 탐색하긴 하지만 현재 State 에서 Goal 까지의 path cost를 구할 수 없기 때문에 모든 방향으로 뻗어나가기도 하고 무한 루프에 빠질 수도 있었습니다.
Informed Search는 이러한 단점을 극복하기 위해 탄생한 탐색법입니다.
Informed Search 의 장점은 Solution 을 더 일찍 효율적으로 찾을 수 있기 때문입니다. 대체적으로 Uninformed Search 보다 효율적입니다.
Informed Search의 기본적인 접근 방법은 Best-First Search 입니다. 다 기반이라고 생각하시면 됩니다.
Best-First Search 는 평가 함수 F(n) 을 기반으로 한 Tree/Graph-Search 의 확장입니다.
이는 Uninformed Search의 Uniform-Cost Search 와 유사한데 Uniform-Cost Search는 현재 노드에서 탐색하는데 가장 비용이 적게 드는 노드로 탐색을 진행합니다. Best-First Search는 비용계산을 G(n) 대신 F(n)을 사용하는 겁니다.
평가 함수 F(n) 은 G(n) 과 H(n) 으로 이루어져 있습니다. n 부터 Goal state 까지의 비용(=거리) 입니다.
여기서 G(n) 은 현재 노드에서 가장 가까운 거리를 찾는거고
H(n) 는 현재 노드에서 목표 노드까지의 거리를 계산한 겁니다.
예를 들어 현재 위치가 목표 노드이면 H(n)은 0이 되겠죠.
Informed Search 중에 두 가지 종류 Greedy Best-first Search 와 A* Search 를 알아봅시다.
1. Greedy Best-first Search
2. A* Search
이 중에 가장 유용하고 실제로 많이 사용되는 건 A* Search 라고 합니다. 그리고 Heuristic Search 는 길찾기 알고리즘에 많이 사용된다고 합니다.
아래 지도로 Informed Search 에 대해 알아봅시다.

1. Greedy Best-First Search
그리디는 '탐욕적인'이라는 뜻입니다. 현재 상황에서 가장 좋아보이는 걸 선택하여 최적인지 아닌지는 항상 확인을 해줘야하는 알고리즘이죠. 여기서는 평가함수가 오직 H(n) 으로 구성됩니다.
(G(n)으로만 구성되면 Uninform Search의 Uniform-Cost Search입니다.)
F(n) = H(n)
휴리스틱 함수는 위에도 말했듯이 현재 노드에서 목표 노드까지의 거리를 계산한 겁니다. 이 함수는 어떻게 설계하냐에 따라 알고리즘의 효율성이 정해지겠죠. 보통 길찾기에서는 H(n)을 현재 노드와 목표 노드 사이의 직선 거리로 확인한다고 합니다. (실제로 장애물들을 효과적으로 건너가서 길을 찾는 프로그램들이 사용하는 알고리즈이라고 합니다.)
SLD : Straight-Line Distance between n and the goal location
SLD 는 n 노드( = 현재노드) 와 goal node 와의 거리입니다.

SLD를 휴리스틱으로 정합시다.
이제 Arad라는 도시에서 Bucharest 까지를 Greedy Best-First Search 로 이동해 봅시다.
Tree-Based Search 를 사용하면 다음과 같습니다.
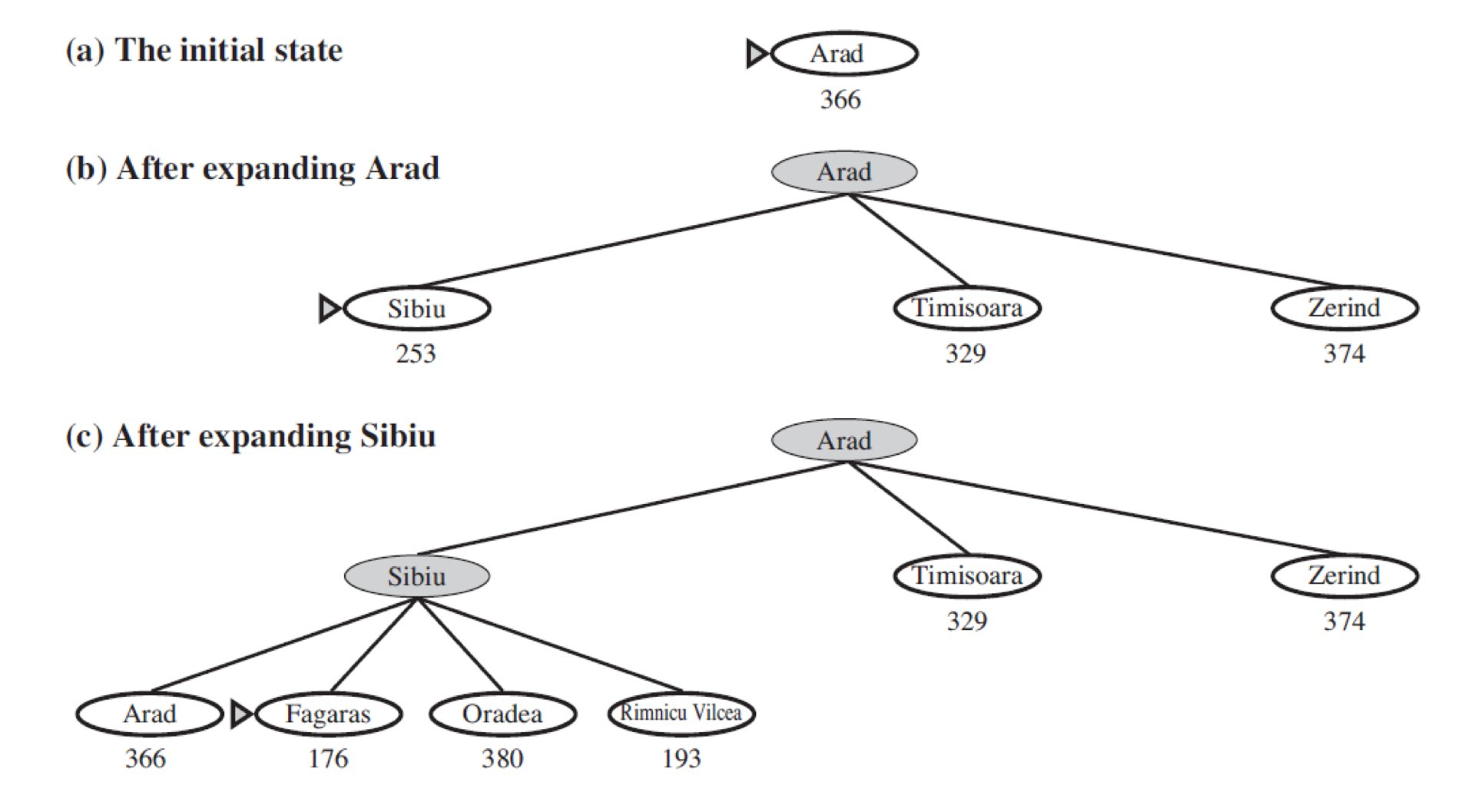
*각 노드 사이의 거리가 아니라 목표 노드까지의 직선 거리임을 알 수 있습니다.
또한 (c) 단계에서 arad 가 다시 한 번 나오는 것을 볼 수 있습니다.
하지만 여기서 다시 arad 에 들어가면 무한 루프를 돌 수 있기 때문에 Node 를 Expand 할 때 자신의 조상 노드를 확인하여 이미 방문한 노드라면 Discarding 해줘야합니다.
Evaluation
Complete : X
Optimal : X
Time & Space Complexity : O(b^m)
- 만약 휴리스틱 함수 알고리즘을 적절하게 썼을 경우 복잡도를 줄일 수 있습니다.
또한 Graph Search 를 사용하여 Search Space 가 유한한 경우에는 Complete 하다는 결론을 낼 수 있습니다.
2. A* Search
A* Search 는 F(n) 함수로 H(n) 뿐만 아니라 G(n) 도 사용합니다.
F(n) = H(n) + G(n)
한번 더 강조하지만 G(n) 은 시작 노드에서 현재 노드까지 걸린 Path Cost 이고 H(n) 은 현재 노드에서 골 노드까지의 가장 빠른 길입니다.
따라서 F(n) = H(n) + G(n) 은 n을 통한 Solution 중 가장 적은 비용을 추정하는 방법이라고 할 수 있습니다.
결과적으로 이 A* Search 는 Optimal 하고 Complete 합니다.
이는 Uniform-Cost Search 와 크게 차이가 없습니다. 단지 평가 함수에 차이가 있는 거죠.
중요한 건 휴리스틱 함수, H(n) 함수입니다. 어떤 방식을 사용하느냐에 따라서 최적해를 구할 수 있는지 없는지가 결정되기 때문입니다.
최적화(Optimality)를 위해서는 2가지 조건이 요구됩니다.
1. Admissibility (객관성)
H(n) 가 Admissible 휴리스틱이어야합니다. 이는 '인정 가능한' 이라는 의미가 있는데 즉, 아주 객관적인 휴리스틱을 설정해서 누구나 인정할 수 있어야한다는 의미입니다. 이 휴리스틱의 예시로 위에서 Greedy Best-First Search 에서 SLD는 휴리스틱을 목표노드까지의 직선 거리로 잡았습니다. 직선 거리로 잡았기 때문에 이 보다 거리가 짧을 수는 없습니다. 그렇기 때문에 객관성을 인정 받을 수 있습니다. 휴리스틱을 한 바퀴 돌아서 잡으면 객관적이지 않기 때문에 Admissibility 를 만족하지 못합니다.
2. Consistency (일관성)
현재 노드를 N , 행동 A를 통해 얻은 자식 노드 중 하나를 P
라고 할 때 N에서 Goal 까지의 거리인 H(N) 은 N에서 P 까지의 거리, C(N,P)와 P에서 Goal 까지의 거리인 H(P) 의 합보다 작아야합니다. 이는 당연한 소리인데 '서울'에 있는 내가 골 노드인 '부산'으로 갈려고 해요. 그때 자식 노드인 '경기도'에 들립니다. 그럼 다음이 만족해야 일관성이 유지된다는 것입니다.
'서울' 에서 '부산' 가는 거리 <= '서울' 에서 '경기도' + '경기도'에서 '부산'
Greedy Best-First Search 에서 사용한 SLD도 일관성이 지켜지고 있다는 사실을 알 수 있겠죠
요약하자면
Admissible Heuristic : Goal 까지의 도달 비용이 과대 평가 되지 않는 객관적인 휴리스틱
Consistency Heuristic : H(n) <= C(N,P) + H(P) 를 유지하는 휴리스틱
이라고 할 수 있습니다.

다음은 A* Search 로 탐색한 겁니다.
(G(n) 은 시작 노드에서 현재 노드까지 걸린 Path Cost 이고 H(n) 은 현재 노드에서 골 노드까지의 가장 빠른 길)
ex ) (b)에서 Arad 에서 Sibiu 까지의 Path Cost 는 140 이고 Sibiu 에서 Bucharest 까지는 253 이 걸립니다.

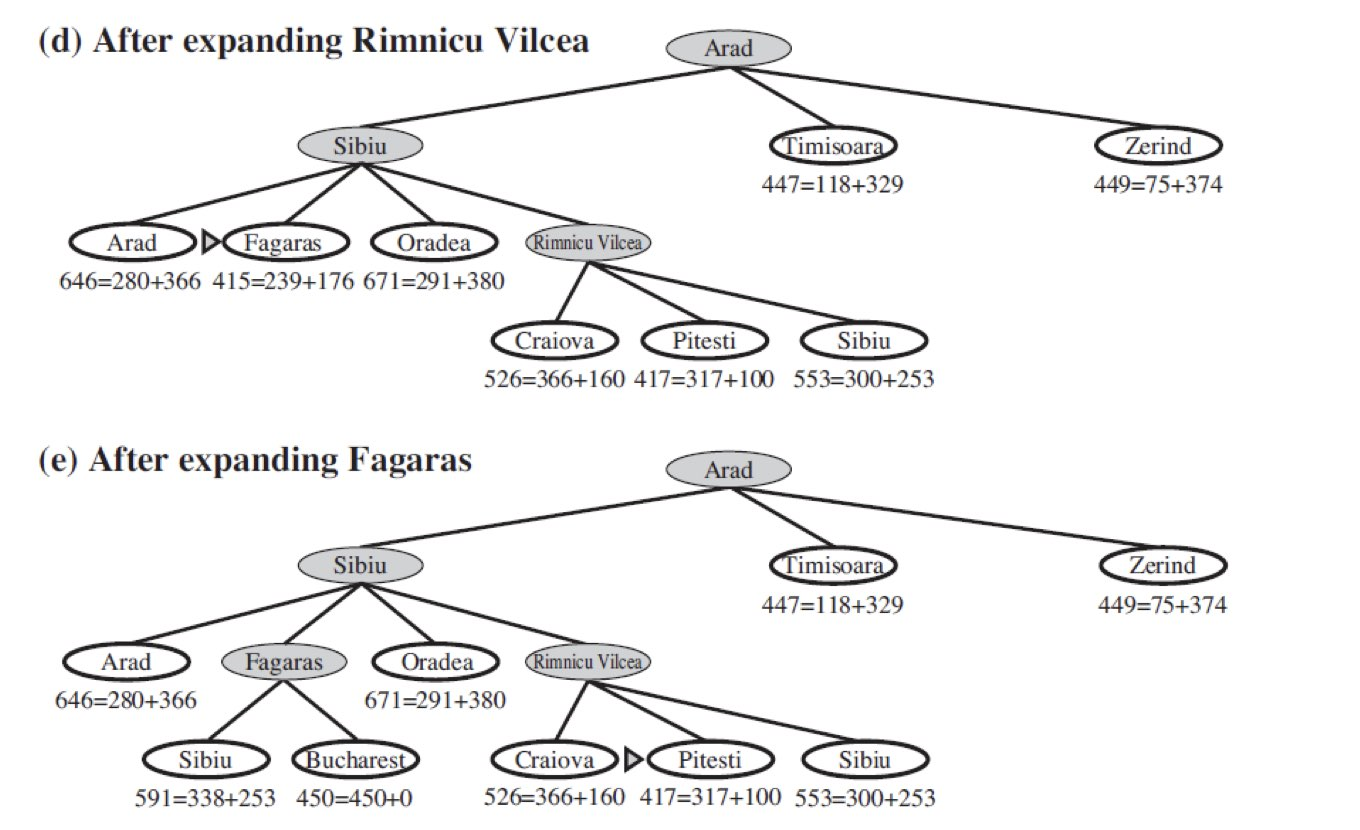
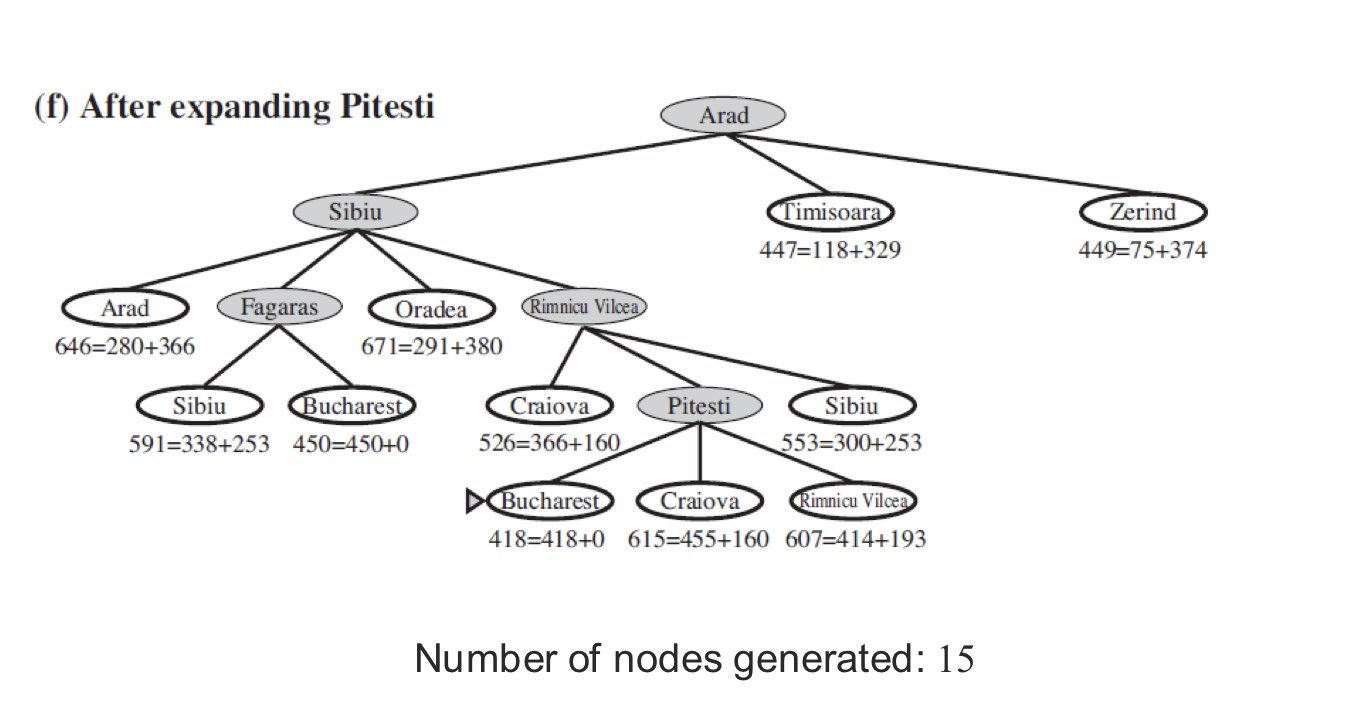
A* Search 의 특징
1. Tree-Search 일 때 h(n)이 Admissible 하면 Optimal 해진다.
2. Graph-Search 일 때 h(n)이 Consistent 하면 Optimal 해진다.
Tree-Search 일때 최적 비용은 C* 라 하고 Goal 이 G1이라고 가정해봅시다.
이 때 최적인 아닌 다른 골 G2가 이라고 하면 최적이 아니기 때문에
F(G2) = G(G2) + H(G2) = G(G2) > C* 입니다. (G2로 도착했기 때문에 H(G2) =0 입니다.)
이 때 G1 가는 길에 노드 하나를 n이라고 합시다.
그럼 결과적으로 F(n) = G(n) + H(n) <= C* 가 성립합니다.
이 또한 당연한 거죠. 결과적으로 F(n) < G(G2) 이기 때문에 A* 이론 상 당연히 G2보다 N이 먼저 Expand 하게 됩니다.
이를 통해 Optimal 함이 보장이 되어 있는거죠.
Admissible 하다는 걸 Goal 에 이르는 길이 과대평가 되지 않는다는 겁니다. 이는 최적 비용 C*를 가진다는 것은 Optimal 을 보장합니다.
Graph-Search 일때도 동일합니다. 이 때 Optimal 을 증명하기 위해서는 Consistent, 일관성이 필요한데 이는 탐색할 수록 비용도 증가해야하는 의미입니다. F(n)은 절대로 감소할 수 없는 평가 함수입니다.
노드 N, N의 자식노드 N' 라고 가정할 때
H(N) <= C(N,N') + H(N')
F(N') = G(N') + H(N') = G(N) + C(N,N') + H(N') -> 시작노드에서 자식노드 N'
F(N) = G(N) + H(N)
이기 때문에
F(N') >= F(N) 은 항상 성립합니다.
약간의 설명을 덧붙여 보겠습니다.
H(N) <= C(N,N') + H(N') 는 Consistent 한 겁니다.
F(N') = G(N') + H(N') = G(N) + C(N,N') + H(N')
-> 시작노드에서 자식노드 N' 까지의 거리 + 자식노드 N'에서 Goal 까지의 거리 = 시작노드에서 노드 N 까지의 거리 + N에서 N' 까지의 거리 + 자식노드 N'에서 Goal 까지의 거리
F(N) = G(N) + H(N)
-> 시작노드에서 노드 N 까지의 거리 + 노드 N에서 Goal 까지의 거리
Consistent 하기 때문에 F(N') 은 늘 F(N) 보다 크거나 같다.
= F(N)은 감소 하지 않는다.

F(N)이 점차 증가하는 것을 알 수 있습니다.
마지막으로 상기 시켜드리자면 다음과 같습니다.
F(n) = G(n) + H(n)
1. H(n)= 0 -> uniform cost search
2. G(n) = 1, H(n) = 0 -> breath-first search
3. G(n) = 0 -> greedy best-first search
Evaluation
Complete : O
Optimal : O
Time Complexity : 휴리스틱 함수에 근거하여 Exponential(지수적인)하다.
Space Complexity : O(b^m)
'공부 > 인공지능' 카테고리의 다른 글
| [인공지능] 6. Karush-Kuhn-Tucker(KKT) Approach (0) | 2020.10.14 |
|---|---|
| [인공지능] 5.Continuous State Spaces & Constrained Optimization Problem (0) | 2020.10.14 |
| [인공지능] 4.Local Search Algorithms (0) | 2020.10.13 |
| [인공지능] 2.Uninformed Search(Blind Search) (2) | 2020.09.28 |
| [인공지능] 1.인공지능 기초 용어 정리 (0) | 2020.09.28 |



