스펙에서부터 상태천이도를 구하는 과정을 알아봅시다.
FSM(Finite State Machine) 상태유한기는 상태가 유한한 회로인데 즉 순차회로라는 뜻입니다.
다음 순차회로는 Binary String에서 특별한 패턴 "1011" 찾는 회로입니다.
1011을 찾으면 출력이 1이 되어야합니다.

ex)01101101100 가 들어옵니다. 01101101100 이 부분과 01101101100 에서 출력 1이 나옵니다.
출력 : 00000100100
이런 식이 되겠죠.
그럼 이러한 동작을 하는 상태천이도를 그려보겠습니다.
순차회로는 두가지 타입이 존재 합니다.
밀리머신(Mealy Machine)과 무어머신(Moore Machine)인데요.
밀리머신 : 출력이 현재상태와 입력에 의해서 결정
무어머신 : 출력이 현재상태에 의해서만 결정
무어머신 먼저 살펴보겠습니다.

상태가 5개 A,B,C,D,E 입니다. 다음과 같습니다.
A : 1011 중 아무것도 못 찾은 상황
B : 1011 중 제일 처음(1)011을 찾은 상황
C : 1011 중 (10)11 을 찾은 상황
D : 1011 중 (101)1 을 찾은 상황
E : 1011 을 다 찾은 상황
그러니 A,B,C,D 의 출력은 0이고 E의 출력은 1이겠죠? 위 그림에 상태 밑에 적힌 숫자의 의미를 알 수 있을겁니다.
각 상태에서 1011을 찾는 것에 실패하는 입력이 들어오면 어느 상태로 가야하는지 결정하면 됩니다.
이게 무슨 말이냐면 예를 들어 설명해보겠습니다.
0 은 1011 이 될 기미도 안보이기 때문에 A 상태입니다. 이 상태에서 0이 들어오면 어떻게 될까요? 여전히 A 상태입니다.
1이 들어오면 B 상태가 됩니다. 1011 을 찾아야하니깐 다음에 0이 들어와야하는데 1이 들어온다면 11 이죠. 그럼 어느 상태가 될까요? 1(1) 이니깐 B상태죠.
10는 C상태입니다. 1011을 찾아야하니깐 다음은 1이 들어와야합니다. 하지만 0이 들어온다면 어떻게 될까요? 100 입니다. B처럼 스스로의 상태가 아니라 다시 처음부터 찾아야하기 때문에 아무것도 못 찾은 A 상태로 갑니다.
101은 D 상태입니다. 1011에서 1만 추가되면 되는 상황입니다. 하지만 0이 들어온다면 1010 이 되죠. 그럼 이건 어떤 상태인가요? 10(10) 이기 때문에 10을 찾은 상태입니다. 이는 C상태이죠.
1011 은 E상태입니다. 이미 찾았음으로 두 상황 다 생각해보겠습니다. 0이 들어오면 101(10) 이 됩니다. 10을 찾은 C 상태가 됩니다. 1이 들어오면 어떻게 되나요? 10111 이므로 1011(1) 이니 1을 찾은 상태인 B상태로 가게 됩니다.
상태천이도는 표 형식으로 바꿀 수 있습니다.

현재상태 입력에 따라 출력이 어떻게 되는지 보여주고 있습니다.
다음은 밀리머신(출력이 현재상태와 입력에 의해서 결정) 의 상태 천이도를 보겠습니다.

밀리머신은 무어머신보다 상태가 적거나 같습니다. 여기서도 5개의 상태인 무어머신보다 상태가 하나 작은 4개입니다.
A : 아무것도 발견 못한 상황
B : 1011의 처음 1을 발견한 상황
C : 1011의 10을 발견한 상황
D : 1011의 101을 발견한 상황
화살표에 그려진 '0/1' 는 '입력/ 현재상태'를 의미합니다.
위에서 과정을 설명했기 때문에 밀러머신의 과정을 이해하시는 것도 어렵지 않으실 거라 생각합니다.
밀리머신도 당연히 표로 나타낼 수 있습니다.

상태할당(State Assignment)에 대해 알아보겠습니다.
상태할당은 심볼 상태에 이진코드를 할당하는 과정입니다.
만일 상태수가 4개이면 최소 2개의 플립플롭이 필요합니다. 5개면 최소 3개겠죠.
이처럼 최소한의 플립플롭을 사용하는 것을 최소 길이 상태할당(minimum length state assignment)라고 합니다.
또 우리가 오늘 집중할 다른 상태할당 방식은 원핫할당(One-hot state assignment)입니다. 원할코딩은 플립플롭을 상태수만큼 사용하는겁니다. 상태가 4개이면 4개의 플립플롭, 5개면 5개를 사용하는거죠.

얼핏보면 one-hot이 쓸데없이 플립플롭을 많이 사용하는 거 같지만 아닙니다.

상태할당을 하고 난 다음에는 조합회로부에서 출력들에 대한 최소한의 논리식 구해야합니다. 그런데 최소길이방식을 사용한 경우보다 원핫 방식을 사용하게 되면 조합회로부에서 출력들에 대한 논리식을 구하는 과정에서 이 논리식들이 훨씬 간단해집니다. 즉 조합회로부가 원핫방식이 최소길이 방식보다 간단하다는거죠.
이유는 4비트로 존재하는 16개의 이진값에서 원핫코드인 다음 숫자를 제외한 나머지
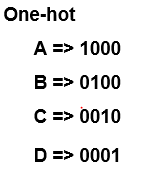
즉 12개의 0000,11--,1-1- 등등의 값을 Don't Care로 처리할 수 있기 때문에 조합회로부가 훨씬 간단해지는 겁니다.
뿐만 아니라 조합논리회로에 대한 논리식을 구하는 경우에도 훨씬 최소화된 논리식을 구할수가 있습니다.



이렇게 상태변수를 생각한다면 순차회로의 구조는 이렇게 됩니다.

one-hot 상태할당의 특징점은
Q3 = 1 이면 상태 A
Q2 = 1 이면 상태 B
Q1 = 1 이면 상태 C
Q0 = 1 이면 상태 D
처럼 조합회로의 식을 구한다는 겁니다.
그럼 이런걸 생각해볼까요?
다음상태가 A가 되는 두가지 조건은 뭔가요?
1. 입력 X = 0 이고 동시에 현재상태가 A
2. 입력 X = 0 이고 동시에 현재상태가 C
-> (A) = X^ AND 현재상태 A, (A) = X^AND 현재상태 C
one-hot 코딩의 특징으로부터 완전한 부울식은
D3 = X^Q3 + X^Q1 입니다.
즉 K-map을 사용하지 않고도 최적화된 부울식을 구할 수 있다는 겁니다.
반면에 최소길이할당을 사용하는 경우에는 최소화된 부울식을 얻으려면 k-map을 사용해야합니다.
뿐만 아니라 얻어진 부울식도 one hot code를 사용한것이 최소길이 코드를 사용한 것보다 훨씬 간단합니다.
간단하는 건 훨씬 적은 코드로 구현이 가능함을 의미합니다!
오늘은 이렇게 원핫코드와 밀리, 무어머신의 상태천이도에 대해 알아보았습니다.
'공부 > 논리회로설계' 카테고리의 다른 글
| 논리회로설계(레지스터 설계 예시, 비동기식 카운터 설계) (2) | 2020.06.22 |
|---|---|
| 논리회로설계(데이터패스,컨트롤 유닛) (0) | 2020.06.16 |
| 논리회로설계(레지스터 전송 수준에서의 논리설계방법) (0) | 2020.06.12 |
| 논리회로설계(레지스터전송수준설계) (0) | 2020.06.10 |
| 논리회로설계(레지스터) (2) | 2020.06.04 |



