https://www.youtube.com/watch?v=Lq8b9yw8uPk
유튜브 설명영상을 찍었습니다! 굉장히 허접한데 발전해 가는 모습 모여드리겠습니다ㅠㅠ
Number Theory 중에서도 보안에서 꼭 알아야하는 'Group'에 대해 알아보겠습니다.
전체적인 집합의 그림은 아래와 같습니다.
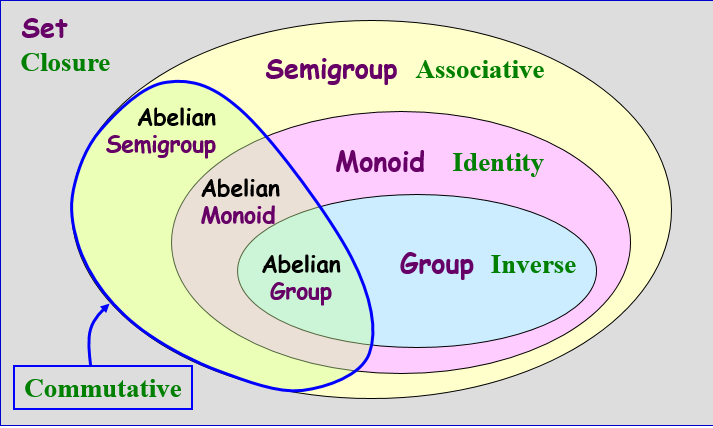
저희는 오늘 Group,Field,Ring에 대해 집중적으로 공부해보도록 하겠습니다.
이러한 집합들은 '어떠한 연산을 만족시키는' 기준으로 집합이 형성됩니다. 여기서 '어떠한 연산'이 존재하는지 알아보겠습니다.
Properties of Operator
⊕ : k X k -> k (하나의 연산자라고 생각을 해주시면 됩니다.)
(1) Closure : 닫혀있다 라는 의미.
집합 {1,2,3} 있을때 연산을 아무리 해도 결과가 {1,2,3} 외 다른 값이 나오지 않으면 이를 'Closure', 닫혀있다라고 표현할 수 있습니다. 실제로 정수에서 아무리 정수를 곱해도 정수로 값이 나옵니다.
(2) Associative : 결합법칙
이미 알고 계실텐데 (a⊕b)⊕c = a⊕(b⊕c) 가 성립하는 겁니다. 수학에선 법칙이지만 우리가 공부하는 Algebra(대수학)에서는 반드시 성립하진 않는 경우도 많습니다.
(3) Identity : ⊕ 연산에 대해 e ∈ K 가 존재

Identity element e 는 항등원이라 불리고 ⊕ 연산에서 자기 자신이 결과값으로 나오게 하는 값을 말합니다.
추가로 Zero element z 는 영원이라 불리고 계산했을때 z 가 나오게 하는 값을 말합니다.

정수에서 '1,2,3' 0을 더해주면 결과 값이 '1,2,3' 으로 자기 자신이 됩니다. 여기서 ⊕연산은 '+' 입니다.
0이 Identity element 입니다.
이와 같이 ⊕연산은 'X' 곱셈으로 두었을때 Identity 1 Zero 0 이겠죠?
1 x 1 = 1 / 2 x 0 = 0 생각해보면 그렇게 어렵지 않습니다.
(4) Inverse : 모든 원소에 대해 각각의 inverse가 존재
⊕ 연산에 있어서 항등원 e 가 되게 하는 연산입니다.

왼쪽, 오른쪽 둘 다 inverse 가 존재할 때 a' 가 a의 inverse 라고 할 수 있습니다.
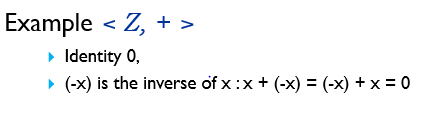
정수에선 항등원이 위에서 말했듯이 0 입니다. 그러면 1의 inverse는?(= 덧셈 을 했을때 0이 되게 하는 값은?)
-1 입니다. 이처럼 (-x)가 inverse 임을 알 수 있습니다.
(5) Commutative : 교환법칙이 존재
a ⊕ b = b ⊕ a
1 + 2 = 2 + 1
2 x 4 = 4 x 2
어렵지 않게 <Z,+> 와 <Z, x> 에서 Commutative 가 성립할 거라는 걸 알 수 있습니다.
(6) Distributive : 분배 법칙 존재

⊗연산에 있어 분배가 성립한다는 의미입니다. 곱셈을 떠올려 생각해보면 쉽게 이해할 수 있습니다.
이렇게 '어떠한 연산'을 다 배워봤습니다.
이러한 연산들을 뭐가 되고 뭐가 안된다는 기준으로 다음 같이 구분이 됩니다.
그럼 'Ring, Group, Field' 에 대해 알아보겠습니다.

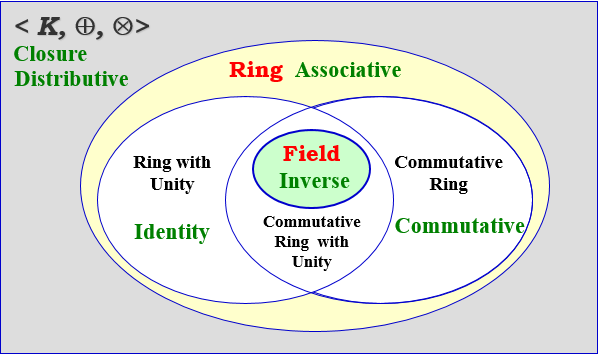
⊗ 도 하나의 연산이라고 생각하면 됩니다. <Z, +, x> 면 정수에서 덧셈, 곱셈이 가능한 집합임을 알 수 있겠죠?
하나의 연산을 쓰는지 두개의 연산을 쓰는지에 따라 둘로 나뉩니다. 전체적으로 비슷한 흐름이고 중요한건 제목과 같이 'Group, Field, Ring' 정도이니깐 미리 겁먹지 않으셔도 됩니다.
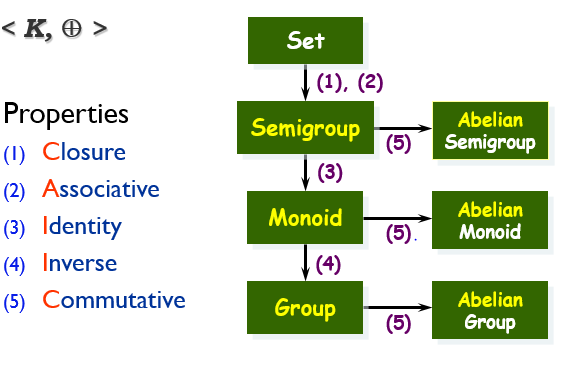
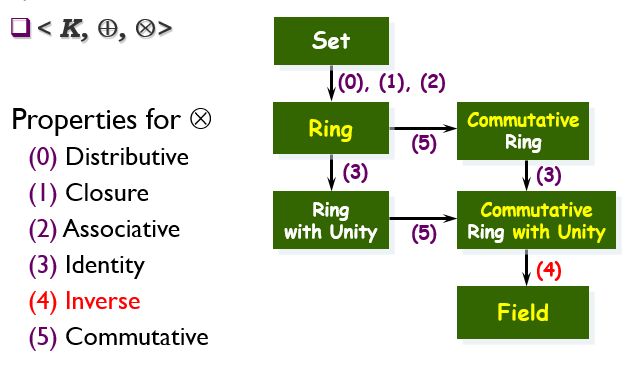
이해를 위해 그림을 더 들고와봤습니다.
(1) Group : Associative, Identity, Inverse 가 <K,⊕> 내에서 성립
< Z , + >
(2) Ring : <K, ⊕ > 에 있어서 abelian group(Group 에서 Commutative 도 성립) 이고 두번째 연산인 <K, ⊕,⊗> 에 있어서 distributive ,associative, distributive (over ⊕) 가 성립
(3) Field : Associative, Identity, Commutative, Inverse
= Ring + Identity,Commutative. Inverse
예를 들어 보겠습니다.

첫번째 연산은 덧셈, 두번째 연산은 곱셈으로 정수, 유리수, 실수, 복소수를 생각한 겁니다. 여기서 정수는 곱셈에 대한 Inverse 가 성립하지 않기 때문에 Ring 입니다. 4 x ? = 1 이 될려면 1/4 이 있어야하는데 이는 정수 범위가 아닌 유리수 있기 때문입니다.
나머지 얘들은 Ring 에다가 inverse 가 존재하기 때문에 Field 라고 할 수 있습니다.
다음 시간에는 조금 더 보안에 관련된 수론에 대해 조금 더 깊게 알아보겠습니다. 수고하셨습니다.
'해킹 > Number Theory' 카테고리의 다른 글
| Chinese Remainder Theorem 중국인 나머지 정리 (0) | 2020.05.26 |
|---|---|
| Carmichael Number&Miller-Rabin Test (0) | 2020.05.25 |
