Carmichael Number&Miller-Rabin Test

안녕하세요. 부산 공수니 입니다. 오늘은 제목과 같이 Carmichael Number 와 Miller-Rabin Test 에 대해 알아보겠습니다. 

 

일단 Fermat's 소정리가 활용되는데요. 모르시는 분은 아래의 포스팅을 확인해주세요!

https://com24everyday.tistory.com/44

Fermat's Theorem/페르마의 정리

 

페르마 소정리에 의하면 만약 p가 prime 일때 1<= a < p 의 모든 a 가 a^p-1 ≡ 1 (mod p) 이고 a^p ≡ a 입니다. 

 

소수를 판단하는 Primality Test 가 있습니다. 하지만 이런 Test로도 소수를 제대로 판별할 수 없는 경우가 존재 합니다. 왜냐하면 페르마 소정리는 필요충분(if and only if) 조건이 아니기 때문에 a^p-1 ≡ 1 이라 할지라도 합성수일 수 있습니다. 예를 들면 341 (11 *31) 도 합성수지만 2^340 ≡ 1 (mod 340) 입니다. 

 

이와 같이 소수가 아닌데 a^(N-1) ≡ 1 (mod N) 을 만족시키는 것을 'passes Fermat test' 라고 표현합니다. 페르마 테스트를 통과한다입니다. 저희는 오직 소수만 이 페르마 테스트를 통과하길 바랍니다. 바람일 뿐이라고요? 아닙니다. 나름 수학적 증거가 있는 소망입니다. 저희는 만약 합성수라면 절반 이상의 a(1 <= a < N) 가 test 에 실패할거라는 걸 알 수 있습니다. 그림을 보며 설명하겠습니다. 

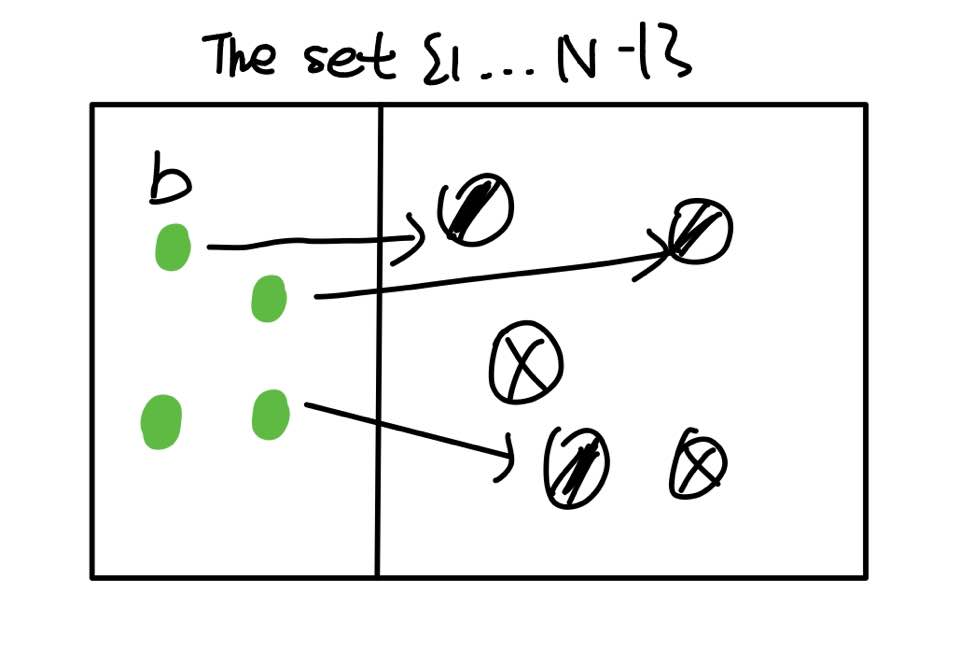
페르마 테스트를 통과한 b에 실패한 a 가 곱해지면 a*b 는 fail 이 됩니다. (ab)^(N-1) =a^(N-1) b^(N-1) = a^(N-1) 이기 때문입니다. 그러므로 매핑을 하게 되면 적어도 pass 하는 수만큼 fail 하는 개수가 존재하게 됩니다. 쉽게 말하면 합성수에서는 fail 되는 게 훨씬 많을 수 밖에 없습니다. 이는 페르마 테스트를 통과한 합성수를 prime 으로 잘못 볼 확률도 1/2 이하라는 것을 의미합니다. 

 

 

-Carmichael Number

 

하지만 모든 a 가 a^(N-1) = 1(mod N) 이 되는 합성수가 존재합니다. 이를 Carmichael Number 라고 부릅니다. 이 수는 N이 합성수일 때도 a^(N-1) =1 (mod N) 이 되는 경우가 많음을 알려줍니다. 10^3 보다 작은 수에선 561 이 있습니다. 그럼 어떻게 소수가 아닐 에러를 줄일 수 있느냐? 검사를 많이 해보면 됩니다! N이 합성수인데 a^(N-1) = 1(mod p) 일 확률이 1/2 보다 작기 때문에 k번 하면 (1/2)^k 번의 확률보다 작아지게 됩니다. 

 

 

 

-Miller Rabin 테스트 설명

Prime Number는 무조건 홀수 입니다. 짝수이면 2가 있기 때문에 소수일 수 없습니다. 

그럼 홀수 N 을 생각해봅시다. 그러면 N-1 은 무조건 짝수이기 때문에 2의 power 형태로 표현이 가능하게 됩니다. 그리고 factoring 을 수행할 수 있습니다. -> N-1 = 2^ek 로 표현할 수 있습니다. 그럼 이런 식이 성립될 수 있습니다. 

 

 

 

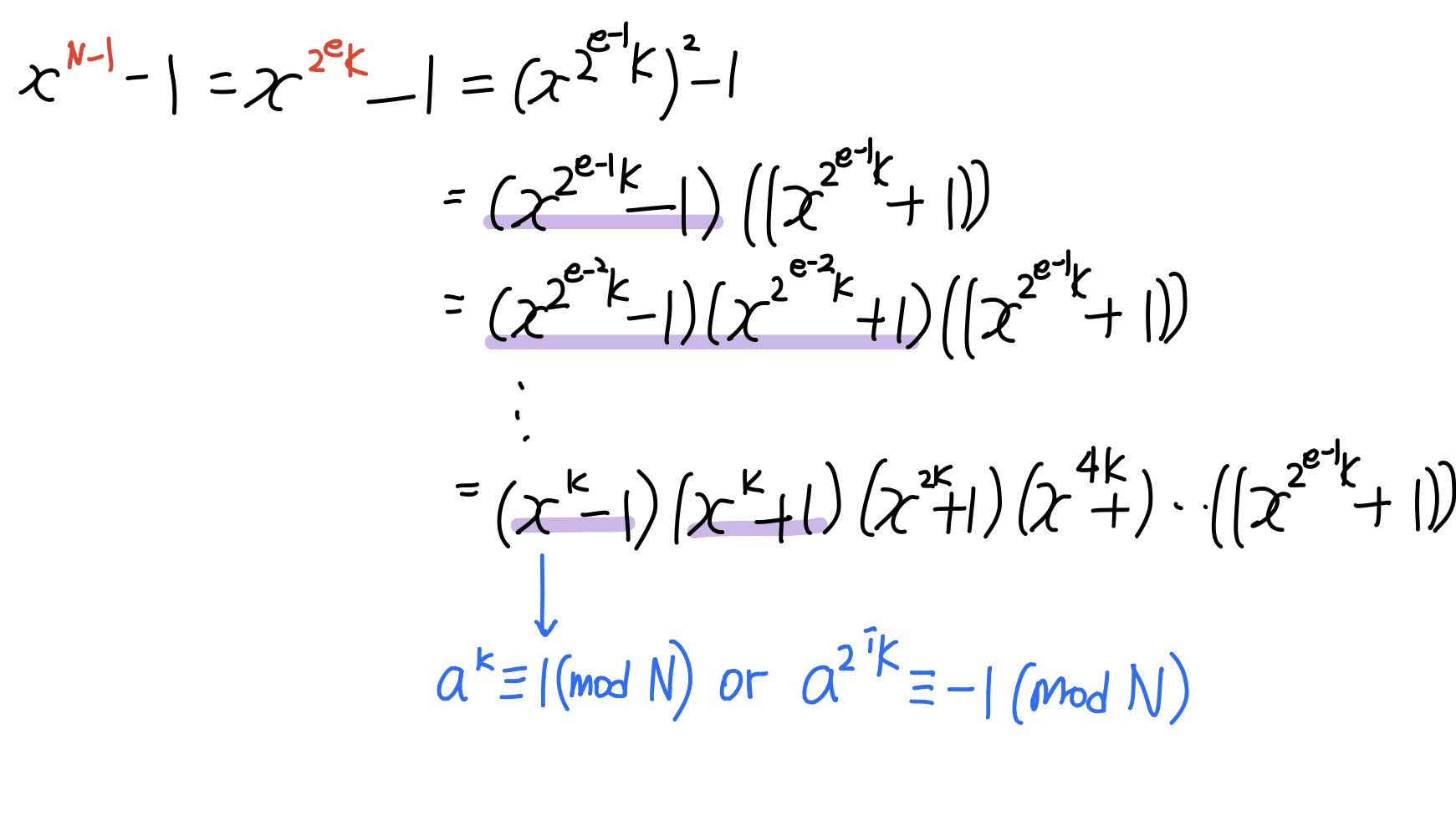
프라임은 a^k = 1(mod N) 또는 a^(2^ik) =-1(mod N)이 무조건 존재해야합니다. 

ex) 

N = 13 

N-1 = 14 

e = 2, k = 3 

a^3 = 1 (mod 13)

a^3 = -1(mod 13) 

a^6 = -1(mod 13)

a는 1 부터 12 까지 

중에 하나는 무조건 만족 시켜야 prime number 입니다.

 

 

ex) Carmichael Number 인 561 로 Miller Rabin 테스트를 진행해보겠습니다. 

 

a = 101 로 선택하고 

560 = 2^4 x 35 

k =35 , e = 4 

a^k = 101^35 = 560(mod 561) = -1

a^2k = 101^ 70 = 1(mod 561) 

-> 초기에 1은 아니었지만 -1 이 나왔습니다. 

 

a = 101 에선 테스트를 통과해서 prime Number 라는 결론을 내릴 수 있지만 이건 Miller-Rabin liar 입니다. 

a = 83 으로 한번 더 시도해봅시다. 

 

a^k = 83^35  = 230(mod 561)

a^2k = 83^70  = 166(mod 561)

a^4k = 83^105  = 67(mod 561)

a^8k = 83^140  = 1(mod 561)

 

-> 1이 나왔기 때문에 561 은 합성수입니다!

 

 

 

이렇게 오늘은 Carmichael Number 와 Miller Rabin Test 에 대해 알아보았습니다. 수고하셨습니다.