저번주에 공부하긴 했지만 이해하는데 좀 시간이 걸리는 바람에 지금 포스팅합니다. 힙정렬은 퀵정렬과 병합정렬과 더불어 시간복잡도 O(nlogn) 을 가진 정렬입니다. 힙정렬을 이해하기 위해서는 완전 이진 트리를 이해해야하는데요. 이진 트리는 자식노드가 두개 이하 트리를 의미합니다..
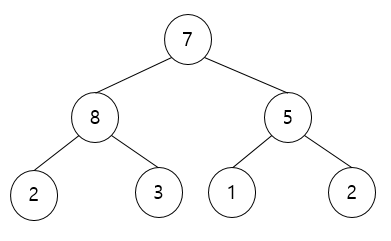
여기서 가장 위에 있는 7은 루트노드(root)입니다. 그리고 8과 5의 부모노드입니다. 2와 3은 8의 자식노드입니다. 가장 밑 부분인 2 3 1 2 는 리프노드(leaf)라고 합니다.
트리는 다양하게 생길 수 있습니다.
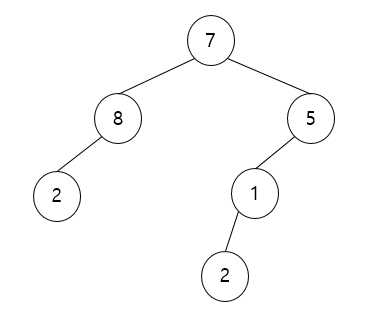
이런식도 가능합니다. 그 중에서 이진 트리는 자식노드가 두개 이하인 트리이고 완전 이진트리는 자식노드가 두개인 트리를 의미합니다. 간단하죠?
힙은 이런 완전 이진트리를 사용합니다.
한번 트리를 만들어 볼까요? 항상 왼쪽 자식 노드부터 데이터가 들어가게 됩니다.
배열 {1,2,3,4,5,6,7,8} 까지 넣어볼까요?
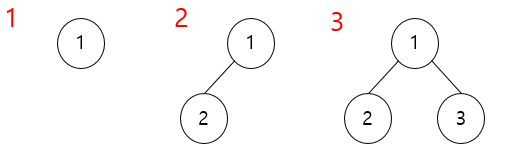
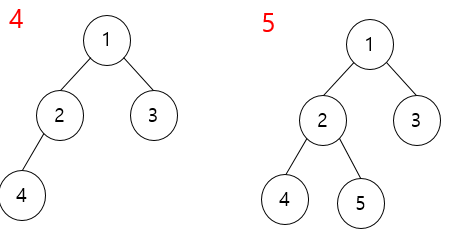
그럼 이제 힙(Heap)에 대해 알아봅시다. 힙은 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리입니다. 힙에는 최대 힙과 최소 힙이 존재합니다. 최대 힙은 부모 노드가 자신 노드보다 큰 힙이고 최소 힙은 부모 노드가 자식 노드보다 작은 힙입니다. 일단 힙 정렬을 하기 위해서는 정해진 데이터를 힙 구조를 가지도록 만들어야합니다.
루트 노드만 생각했을때 이 트리는 힙입니다. 하지만 내부에서 힙이 붕괴된 것을 볼 수 있습니다.
6이 부모 노드인 5보다 크기 때문입니다. 위 쪽은 최대 힙이 맞고 아래는 최대 힙이 아닙니다. 이러면 힙 정렬을 수행할 수 없으니 힙생성 알고리즘(Heapify Algorithm)을 사용해야합니다. 힙 생성 알고리즘은 특정한 '하나의 노드' 에 대해서 수행하는 겁니다. 또한 '하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태'라고 가정을 한다는 특징이 있습니다. 위의 그림이 이 상황에 부합합니다. 5 만 최대 힙 정렬을 실행해주면 전체 트리가 최대 힙 구조로 형성됩니다.
힙 생성 알고리즘(Heapify Algorithm)은 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘입니다. 또한 바꾼 뒤에도 여전히 자식이 존재하는 경우 그 자식 중에서 더 큰 자신과 자신의 위치를 바꾸어야합니다.(재귀 느낌이 들죠?) 위에 예시에서는 5의 두 자식 중 6이 크기 때문에 6과 5를 바꾸어주면 됩니다. 바꾸면 다음과 같아집니다.
모든 부분이 최대 힙이 구성되는 것을 알 수 있습니다. 힙 생성 알고리즘은 전체 트리를 힙 구조를 가지도록 만든다는 점에서 굉장히 중요한 알고리즘입니다. 이러한 힙 생성의 알고리즘의 시간 복잡도는 한 번 자식 노드로 내려갈 때마다 노드의 개수가 2배씩 증가함으로 O(log N)입니다. 만약 데이터 갯수가 1024개 이면 한 10번 정도만 내려가면 된다는 말입니다. 그럼 이제 실제 힙 정렬 과정을 수행해보도록 합시다.
다음 배열을 오름차순으로 정렬해봅시다.
1 2 7 6 4 3 5 9 8
기본적으로 완전 이진 트리를 표현하는 가장 쉬운 방법은 배열에 그대로 삽입하는 겁니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 7 | 6 | 4 | 3 | 5 | 9 | 8 |
삽입되는 순서대로 인덱스를 붙여주는 거라 생각하시면 됩니다. 다음 배열을 완전 이진 트리로 만들면 다음과 같습니다.
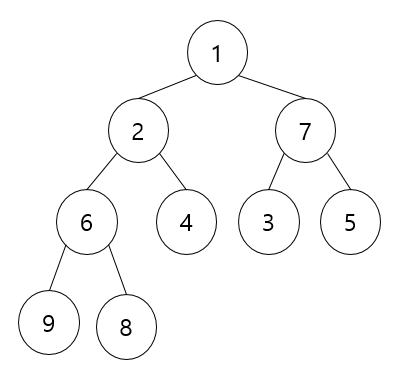
이 트리 구조를 힙 생성 알고리즘을 적용해서 전체 트리를 힙 구조로 만들어주시면 됩니다. 이때 전체 트리를 힙 구조로 만드는 복잡도는 O(N* log N) 입니다. ( 사실 모든 데이터를 기준을 힙 생성 알고리즘을 쓰지 않아도 되기 때문에 O(N)에 가까운 속도를 낼 수 있습니다.)
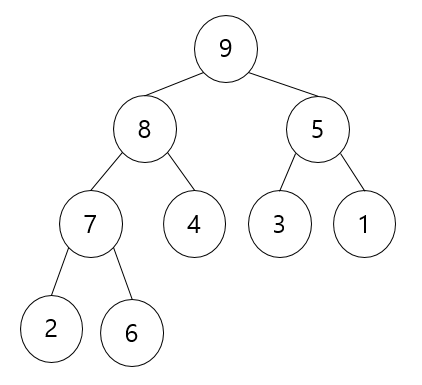
다음과 같은 최대 힙이 구성됩니다. 이렇게 만들어주고 난 다음에 우리가 원하는 정렬을 수행할 수 있게 됩니다. 루트 에 있는 값을 가장 뒤쪽으로 보내면서 힙 트리의 크기를 1씩 빼주는 겁니다.

가장 뒤 쪽에 있던 6과 루트 노드였던 9를 교환해주고 9는 힙에서 사라지는 겁니다. 배열의 현재 상황은 다음과 같습니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 6 | 8 | 5 | 7 | 4 | 3 | 1 | 2 | (9) |
그러면 이런 트리는 지금 루트 노드가 6이니깐 최대 힙 구조가 붕괴되었으니 다시 힙 생성 알고리즘을 진행해줍니다. 그럼 다음과 같이 됩니다.
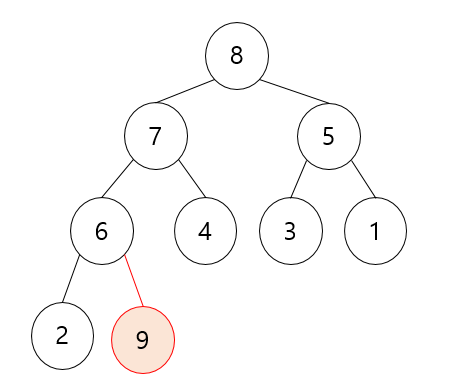
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8 | 7 | 5 | 6 | 4 | 3 | 1 | 2 | (9) |
여기서 제일 뒷쪽 원소(2)와 루트 노드(8)를 바꿔줍니다.
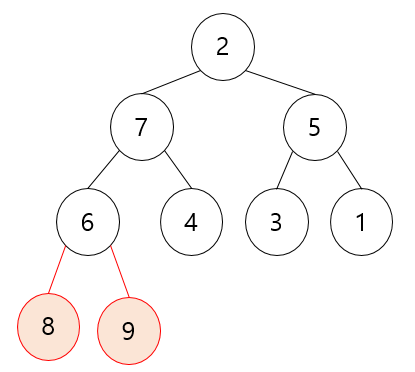
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 7 | 5 | 6 | 4 | 3 | 1 | (8) | (9) |
다시 힙 생성 알고리즘을 해줍니다.
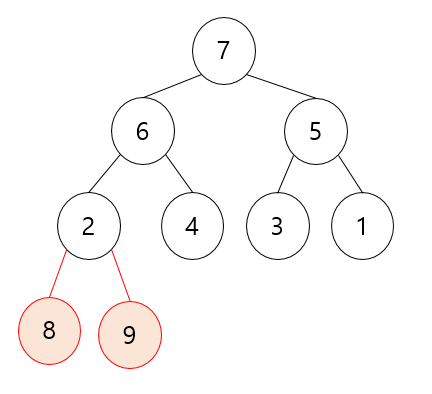
이런 식으로 계속 반복하면 됩니다. 맨뒤에 8 9를 보면 정렬이 이루어지고 있다는 게 보이시죠?
힙 생성 알고리즘의 시간 복잡도는 O(log N)이고 전체 데이터의 개수 N 에 의해 시간복잡도는 O(N * logN) 이라고 할 수 있습니다. ( N번의 힙 생성 알고리즘을 돌려주어야하니깐요) 또한 맨 처음에 힙 구조를 만드는 복잡도는 O(N*logN)이었습니다. 즉 전체 힙 정렬의 전체 시간 복잡도는 O(N * logN) 입니다. (상수는 시간복잡도에선 취급하지 않습니다.)
c 언어 힙 정렬 구현
#include <stdio.h>
int num = 9;
int heap[9] = { 7,3,1,2,4,8,9,0,10 };
int main(void) {
int temp;
//전체 트리 구조를 최대 힙 구조로 바꿉니다.
//부모 노드로 이동하면서
for (int i = 1; i < num; i++) {
int c = i;
do {
int root = (c - 1) / 2;
if (heap[root] < heap[c]) {
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c = root;
//반복문이지만 재귀적 구조
} while (c != 0);
}
//크기를 줄여가며 반복적으로 힙을 구성
for (int i = num - 1; i >= 0; i--) {
//가장 큰 값을 제일 뒤로 보냄 -> 오름차순 정렬
int temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
int root = 0;
int c = 1;
//힙구조 만들기
do {
c = 2 * root + 1;
//자식 중에 더 큰 값 찾기
if (heap[c] < heap[c + 1] && c < i - 1) {
c++;
}
//루트보다 자식 값이 더 크다면 교환
if (heap[root] < heap[c] && c < i) {
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < i);
}
for (int i = 0; i < num; i++)
printf("%d ", heap[i]);
}
힙 정렬은 병합 정렬과는 다르게 별도 추가 배열이 필요하지 않는다는 점에서 메모리 측면에 몹시 효율적입니다. 그리고 항상 O(N * log N) 을 보장할 수 있다는 점에서 강력한 정렬 알고리즘인거죠. 이론적으로는 퀵정렬, 병합 정렬보다 뛰어나지만 단순히 속도만 보면 퀵정렬이 더욱 빠르기 때문에 일반적으로 힙 정렬이 많이 사용이 되지는 않습니다.
*다음 글은 동빈나님의 유튜브를 참고하여 제작된 포스팅입니다.*
https://www.youtube.com/watch?v=iyl9bfp_8ag&list=PLRx0vPvlEmdDHxCvAQS1_6XV4deOwfVrz&index=11
'공부 > 알고리즘' 카테고리의 다른 글
| 알고리즘 스택, 큐 (0) | 2020.06.03 |
|---|---|
| 계수 정렬(Counting Sort) (0) | 2020.06.01 |
| C++ Sort() 사용 (0) | 2020.05.30 |
| 병합정렬 복습 (0) | 2020.05.29 |
| 퀵정렬 복습 (0) | 2020.05.28 |


