이때까지 배운 O(N log N)의 시간복잡도인 선택, 버블, 삽입 정렬 그리고 O(N^2)의 시간복잡도인 퀵, 병합, 힙 정렬을 배웠습니다. 가장 빨랐던 정렬은 아무래도 퀵정렬이었는데요. 이거보다 빠르게 정렬을 하는 계수 정렬에 대해 알아보겠습니다.
다음의 5 이하 자연수 데이터들을 오름차순 정렬하세요.
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
정렬할 데이터 개수가 30개입니다. 특징은 모든 데이터가 1부터 5 사이입니다. 계수 정렬은 이처럼 적절한 '범위 조건'이 있어야한다는 전제에서 굉장히 빠른 알고리즘입니다. 그 속도는 O(N) 입니다. ( 저도 처음보는 시간복잡도의 속도입니다.)
계수 정렬(Counting Sort)는 단순하게 '크기를 기준으로' 세는 알고리즘입니다.
무슨 말이냐면 이 알고리즘은 '크기를 기준으로' 인덱스별로 수를 세어주면 되기 때문에 배열 위치의 교환이 필요가 없습니다. 또한 모든 데이터에 한번씩만 접근하면(O(N) 이 되는 이유) 되기 때문에 굉장히 효율적입니다.
0. 초기상태
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
| 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 |
1. 1번째
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 0 | 0 | 0 |
2. 2번째
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 0 |
3. 3번째
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 1 |
이런 식으로 쭉 해당 크기의 원소를 만ㄷ나는 경우 개수를 하나씩 올려주면 됩니다. 다음과 같은 방식으로 끝까지 진행을 하게 되면 결과는 다음과 같습니다.
1 3 5 2 3 1 3 4 4 3 4 2 3 4 3 1 1 2 4 3 3 1 2 3 4 5 1 3 2 4
| 1 | 2 | 3 | 4 | 5 |
| 6 | 5 | 10 | 7 | 2 |
이제 해당 크기 1부터 5까지 나온 횟수만큼 출력을 해주면 됩니다. 1은 6번, 2는 5번, 3은 10번, 4는 7번, 5는 2번 출력을 해주면 되는 거죠.
1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 5 5
이렇게 출력이 됩니다.
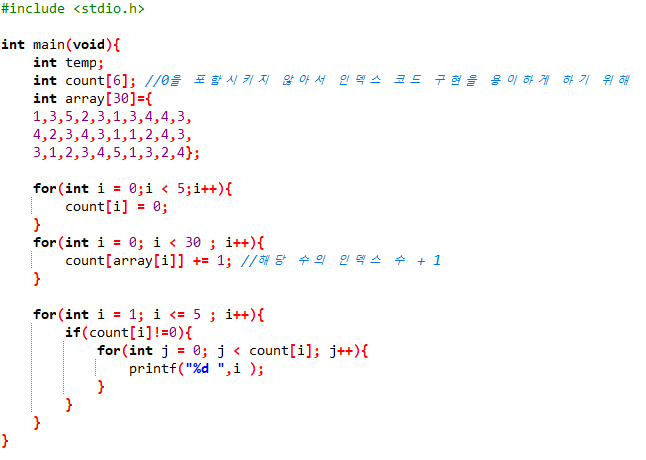
범위 조건이 충족이 될때 쓰기 좋은 알고리즘 코드 입니다. 물론 갑자기 크기가 10000 인 원소가 하나있다면 count의 인덱스가 count[100001] 이런식이 돼서 메모리 낭비가 심해지기 때문에 활용도가 높은 알고리즘이라고 할 수는 없습니다.
'공부 > 알고리즘' 카테고리의 다른 글
| 너비 우선 탐색(BFS) (0) | 2020.06.03 |
|---|---|
| 알고리즘 스택, 큐 (0) | 2020.06.03 |
| 힙정렬 (0) | 2020.06.01 |
| C++ Sort() 사용 (0) | 2020.05.30 |
| 병합정렬 복습 (0) | 2020.05.29 |


