블록암호(Block Cipher)
: 자료 블록을 처리하는 핵심 알고리즘과 운영 모드의 조합으로 구성되는 암호의 한 종류
즉, 일련의 자료 블록들을 처리하는 기법
자료 블록을 처리하는 핵심 알고리즘
- 암호화 알고리즘(E) : 키 K와 평문 블록 P -> 암호문 블록 C 산출 : C = E(K,P)
- 복호화 알고리즘(D) : P = D(K,C)
보안 목표
'얼마나 무작위하게 보이는가?'
블록 암호가 안전하려면 반드시 의사무작위 치환(Pseudo random permutation, PRP) 에 해당해야함.
: 키를 알지 못하는 공격자가 블록 암호의 출력을 계산할 수 없어야 함
P에 대한 E(K,P) 가 어떤 모습일지 단서 없고 그 어떤 패턴도 발견할 수 없어야 함.
블록 크기
블럭 암호 특정 짓는 두 개 수치
-블록의 크기
-키의 크기
보안성은 이 두 값에 의존한다.
64비트(DES) or 128비트(AES) 블록 사용
컴퓨터 계산에서는 2의 거듭제곱을 사용하는데 이는 자료 처리, 주소접근의 편리함 때문입니다.
2^6, 2^7 쓰는 이유는?(2^4, 2^16 아닌 이유)
암호문의 길이와 메모리 사용량 최소화
-> 블록 너무 커서는 안됨
중요) 비트가 아닌 블록은 다름
ex) 128 비트 블록 사용하는 블록 암호로 16비트 암호화 할려면
16비트 -> 128비트로 변환해야함
메모리 사용량(memory footprint)
512비트보다 크면 구현의 비용과 성능이 눈에 띄게 영향
코드북 공격(codebook attack)
블록이 작으면 당함, 참조 공격
블록이 16비트일 때 코드북 만들기 위해 메모리는
2^16 * 16 = 2 ^ 20비트 즉 128킬로바이트
-> 큰 비트면 걱정 안 해도 됨
블록 암호 구성
기법은 적음
실제 쓰이는 블록 암호는 짧은 라운드를 반복하는 형태의 알고리즘
하나의 라운드 구축
1. AES에서의 대입-치환 네트워크(substitution-permutation network,SPN)
2. DES에서의 파이스텔(Feistel scheme)
블록 암호의 라운드
명세와 구현이 쉬운 기본적인 형태의 변환
이 라운드를 여러 번 반복하는 것으로 구성
ex) 평문 세 개의 라운드로 암호화하는 블록 암호는 각 라운드마다 역함수도 존재
라운드 함수들(R1,R2) 는 동일한 알고리즘 사용
라운드 키라고 부르는 값으로 매개변수화
서로 다른 라운드 키 가진 두 라운드 함수는 다른 방식으로 행동
= 같은 입력 다른 결과
(보안성을 올리기 위해서)
라운드 키는 주 키 K로 부터 만들어 낸 키
바꾸는 알고리즘을 키 스케줄(Key Schedule) 알고리즘라고 한다.
이 알고리즘은 라운드마다 다른 키를 부여한다.
슬라이드 공격과 라운드 키
라운드 키가 다르지 않으면 슬라이드 공격(Slide attack) 당함
슬라이드 공격이란
공격자는 P2 = R(P1) 를 만족하는 두 평문쌍 (P1, C1) , (P2, C2) 조사한다.
R은 해당 블록 암호의 라운드 함수다.
라운드가 동일하면
P2 = R(P1) -> C2 = R(C1)
관계 성립
이를 키 복원에 활용된다.
라운드 키의 장점은 부채널 공격을 막을 수있다는 것이다.
그러나 단반향(비가역적) 키 스케줄 알고리즘을 사용하는 블록 암호는 많지 않다.
대입 치환 네트워크
혼돈(confusion) : 입력(평문과 암호키) 가 변환 , 깊이
확산(diffusion) : 혼돈 후 변환들이 입력의 모든 비트에 동일하게 의존 , 너비
블록 암호 설계에서 이들은 대입 연산과 치환 연산 형태
대입치환 네트워크는 두 연산의 결합임.
대입 연산은 S-box로 구현됨. 이는 최대한 비선형적이어야하고 통계적 편향이 없어야 함.
치환은 이에 반해 그냥 비트 순서를 바꾸는거.
어떤 암호는 선형 대수와 행렬 곱셈 이용해 비트 섞음
확산 강해짐
핵심은 초기 상태 모든 바이트가 최종 상태 모든 4바이트에 영향
파이스텔 방안(Feistel scheme)
1. 64비트 반 L,R
2. L = L XOR F(R) F는 대입-치환 라운드
3. L과 R swap
4. 2,3을 15회 반복
5. L,R 을 연결해서 64비트 출력 블록 만듦.
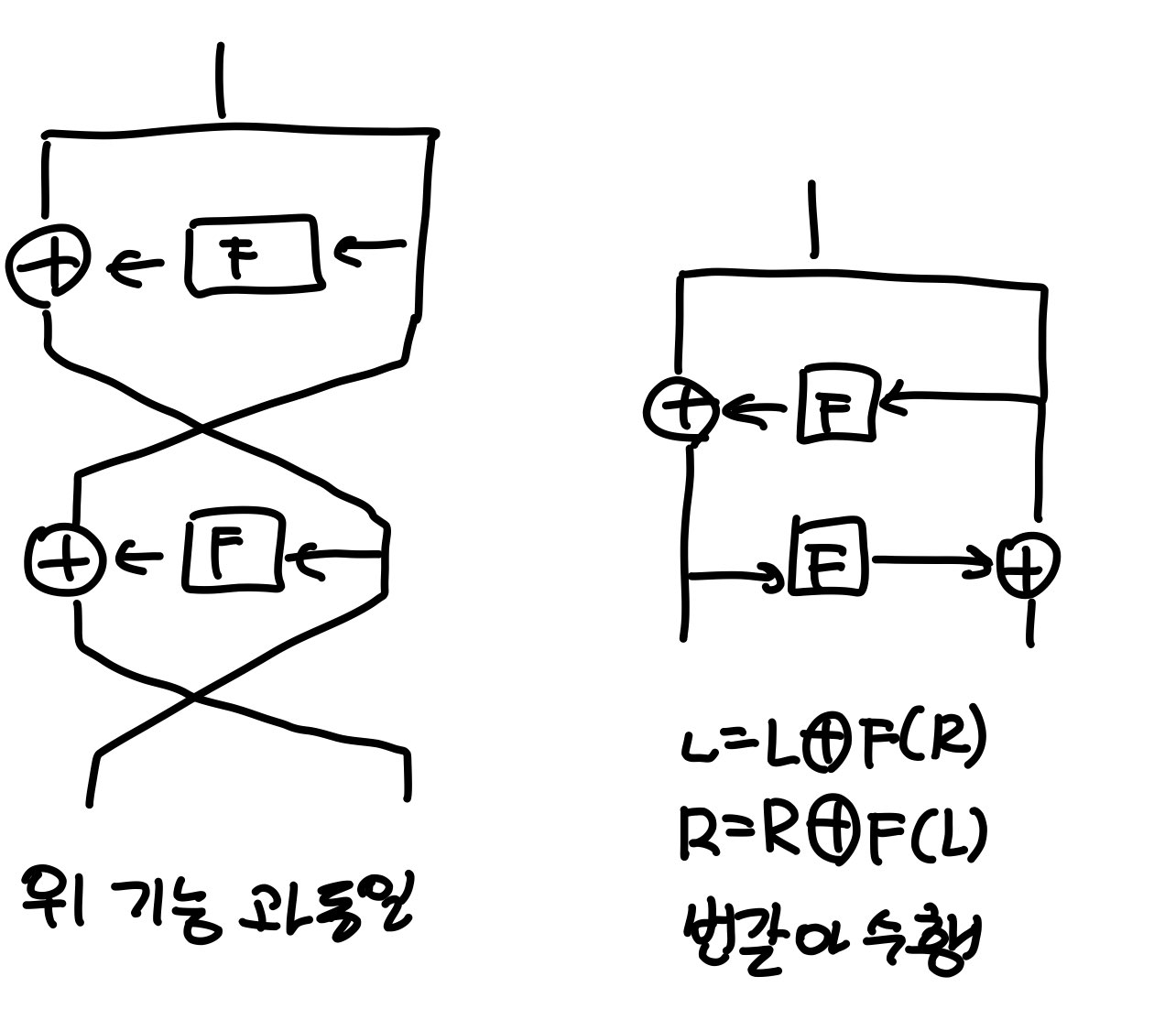
첫번째 F는 K1 라운드키
두번째 F는 K2 라운드키
DES에서 함수는 의사무작위 치환(PRP) 혹은 의사난수함수(Pseudo random function,PRF)
PRP : 다른 두 입력, 다른 두 출력
PRF : F(X) = F(Y) 존재 가능 , 단 F 가 강해야함.
AES(Advanced Encryption Standard)
고급 암호화 표준
현재 세상에서 가장 많이 쓰이는 암호
레인달(Rijndael) 알고리즘 사용
AES 내부
128,192,256 비밀키 하나 이용해 처리
128비트는 조금 더 빠르고 대부분 128비트, 256비트 보안성 차이는 무의미함 .
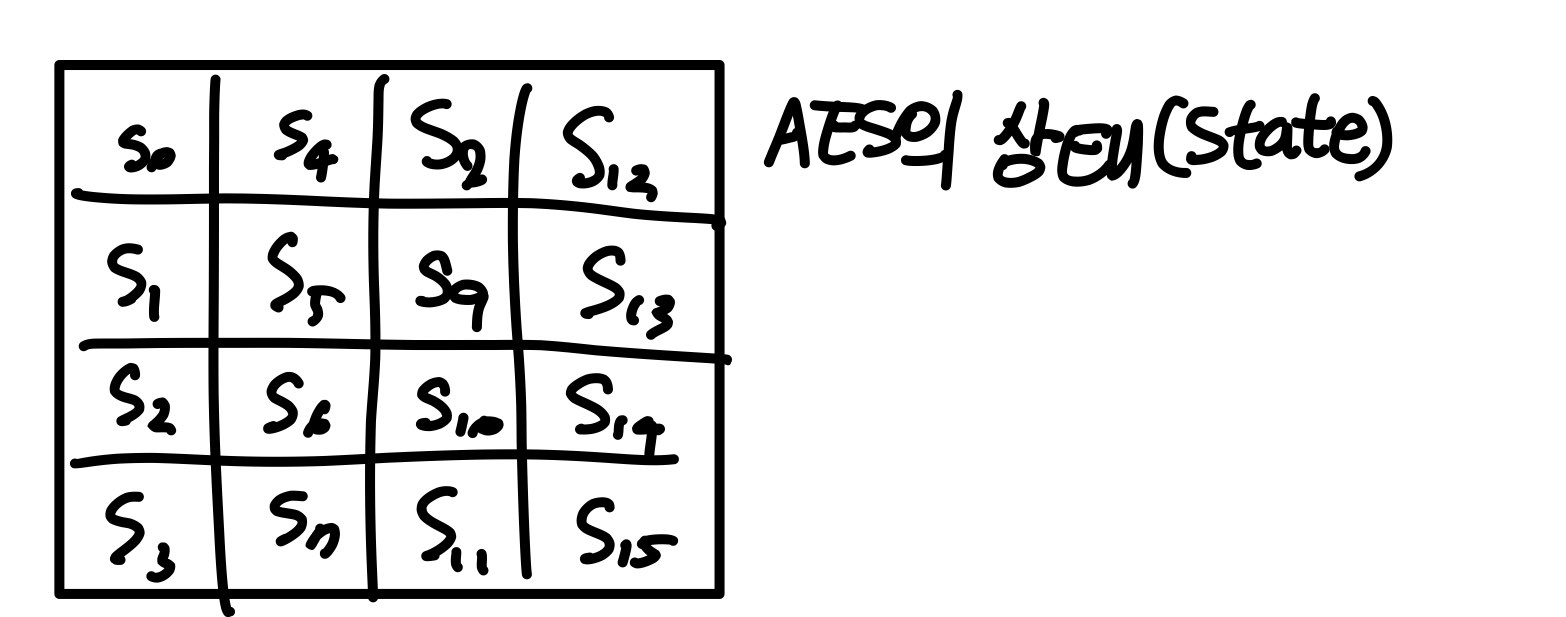
AES는 바이트들을 다룬다.
평문 2차원 배열 취급
AES는 SPN(대입-치환 네트워크)와 다수 라운드 사용해 자신의 상태 변환함.
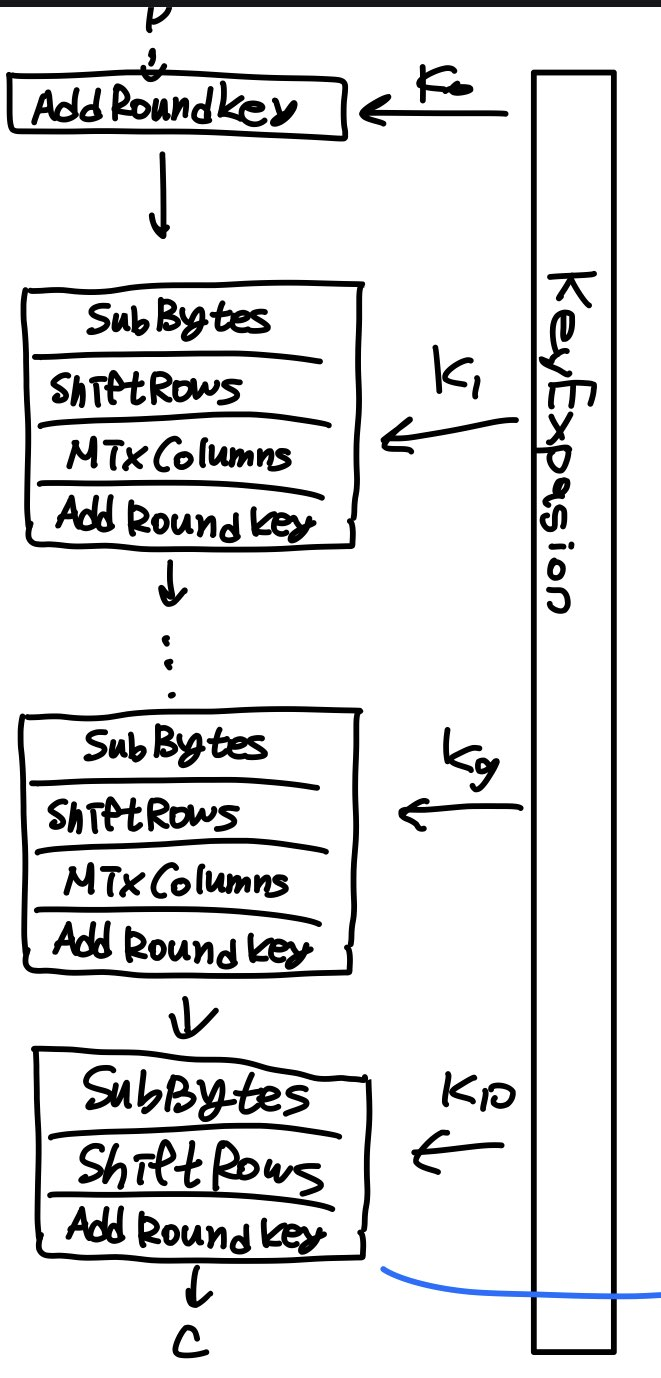
키 스케줄 함수
중요한 속성은 공격자가 라운드 키 Ki 를 알면 알고리즘을 뒤집어 적용할 수 있어 다른 모든 라운드 키 뿐만 아니라 주 키 K도 알아낼 수 있다. 이는 부채널 공격에 대한 보호가 불완전하다는 뜻으로 간주된다.
마지막 과정에 Mixcolumns 연산이 없는데 어차피 선형 연산이기 때문에 예측이 가능하니 안 넣어도 된다.
Add Round key : 라운드 키와 내부 상태 XOR
SubBytes : 각 바이트 (S0,S1,S2,..,S15) 를 S-box 에 따라 다른 바이트로 대체
Shift Rows : 0~3 까지의 i 에 대해 i 번째 행 i자리만큼 순환 이동
MixColumns : 네 열에 대한 동일한 선형변환 적용
각 연산은 AES의 보안성에 각자 나름의 방식으로 기여
-Key Expansion 이 없으면 모든 라운드가 동일한 k를 라운드 키로 사용할 것이므로 AES 는 슬라이드 공격에 취약
-Add Round Key 가 없으면 암호화가 키에 의존하지 않음, 누구나 키 없이도 암호문 복호화가 가능
-SubBytes 는 비선형 연산들을 도입함으로써 암복호화의 강도를 높인다.
이게 없으면 그냥 연립일차방정식이 된다.
-ShiftRow 가 없으면 한 열의 변화가 다른 열들에 영향을 미치지 않는다.
각 열 마다 코드북 만들어서 해결 가능
-MixColumnss 가 없으면 한 바이트의 변화가 다른 바이트들에 영향을 미치지 않는다.
CPA은 256바이트까지 참조표 16개를 이용해서 암호문 복호화 가능
AES 구현
실제로는 테이블 구현(table-based implementation)으로 구현
순차적인 연산열을 XOR 들과 테이블 참조의 조합으로 대신 테이블은 프로그램 자체에 있음
캐시 타이밍 공격(Cache-timing attack) 에 취약
캐시 메모리에서 요소들을 읽거나 기록할 때의 타이밍 변동 활용
이런 시간을 통해 어떤 요소가 접근되는지 짐작 가능
전용 기계어 명령(native instruction)
이의 집합인 AES-NI 통해 캐시 타이밍 공격 여지 없앨 수 있음
하드웨어에서 소프트웨어가 실행되는 방식 생각해야 함
어떤 프로그램 실행할 때 마이크로프로세서는 프로그램의 이진 코드를 집적회로의 구성요소들이 실행하는 일련의 명령들로 번역함
0100101 -( 마이크로 프로세서) -> 일련의 명령어( mov rax,1)
AES-NI 를 사용할 때는 하나의 AES 라운드를 어셈블러 가 아닌 AES ENC 명령을 실행
그러면 마이크로 프로세서가 라운드 계산함.
즉 프로세서는 AES 라운드 실행 명령만 내리면 됨
AES 는 안전한가 ?
모든 출력 비트가 모든 입력 비트에 어떤 복잡하고도 의사 무작위한 방식으로 의존
이때까지 AES를 위협할만한 연구는 나오지 않음
AES의 위협은 알고리즘이 아니라 운영모드에 존재
모드를 잘 선택해도 잘못 사용하면 뚫림
운영모드
1. 전자 코드북 모드(Electronic Code Book, ECB)
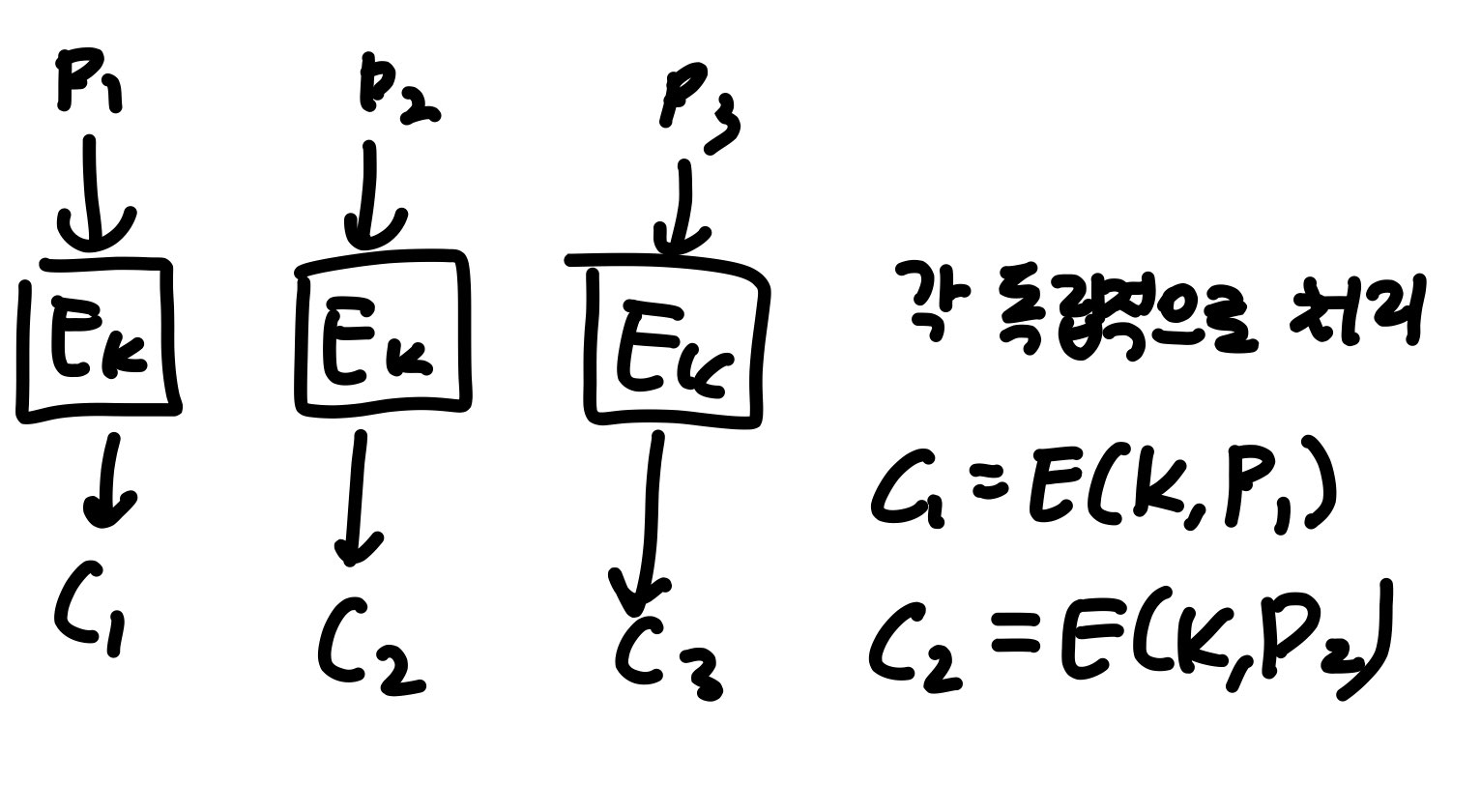
딱 봐도 안전하지 않을 거 같다.
1) ECB 모드에서 공격자가 동일한 암호문 블록들을 통해 평문 식별 가능
2) 전체 블록 단위의 자료들만 처리 가능
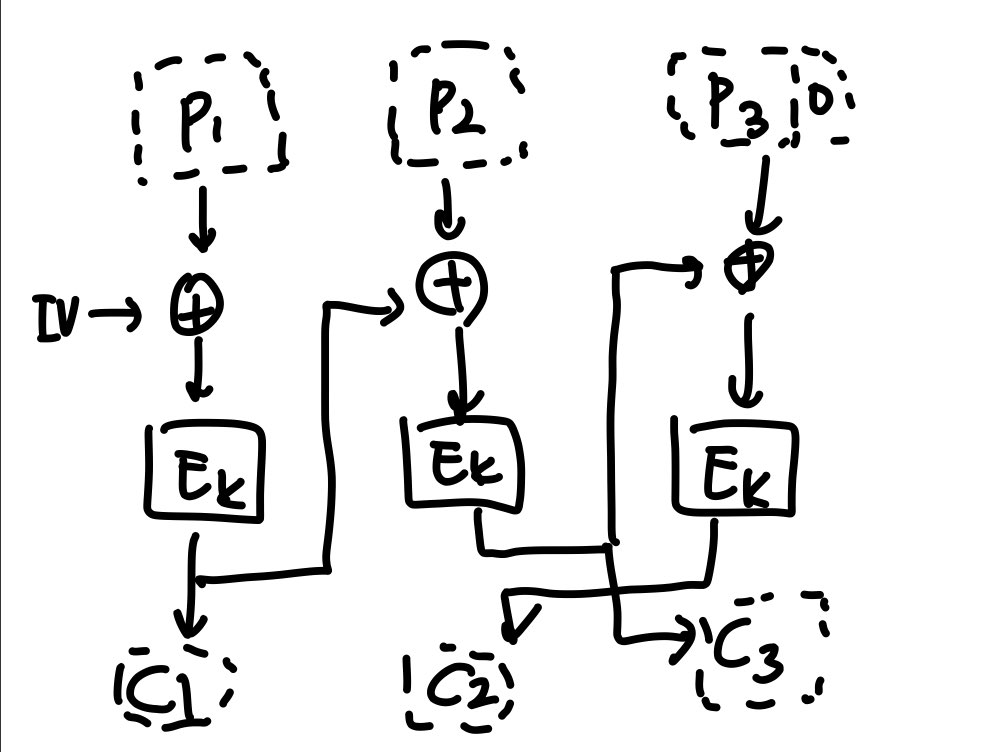
2. 암호 블록 연쇄 모드(Cipher block chaining, CBC)
ECB를 조금 비튼 거임

결과적으로 동일한 평문 블록들이 동일한 암호문으로 암호화 안됨 -> 무작위한 초기치에 의존
허나 고정된 초기치로 CBC를 이용하는 경우가 많기 때문에 평문들이 노출된다.

복호화 할려면 IV 알아야한다. 암호문과 함께 전송
복호화 더 빠름 -> 병렬 처리 가능
Pi = D(K,Ci) XOR Ci-1
이전 평문 블록 Pi-1 가 필요없음
병렬로 한꺼번에 복호화 가능
CBC모드에서 임의의 길이의 메시지를 암호화하는 방법
즉 정수배가 아닌 길이의 평문 처리 방법
16바이트인 AES-CBC 에서 18바이트 평문을 암호화 할려면 어떻게 해야하나
여분 2바이트는 어떻게 처리?
두가지 방법이 있다.
-채우기 (padding) : 암호문이 평문보다 조금 길어짐
-암호문 훔치기(Ciphertext Stealing) : 암호문 평문 길이 같음
1) 메시지 채우기
:어떤 길이도 가능
블록 암호 채움 기법은 HTTPS 비롯한 CBC 쓰이는 거의 모든 곳에 쓰임
마지막 블록이 완전히 채워질 때까지 평문에 여분의 바이트들을 추가
단점은 암호문이 많아야 하나의 블록이 평문의 것보다 적어도 한 바이트 더 길다.
만약 남은 바이트가 1 이면 16 바이트 블록 이니깐 16 - 1 = 15, 0f( 십진수로 15) 인 바이트 15개를 메시지 끝에 추가해서 블록을 채운다.
남은 바이트가 2 이면 16 - 2 = 14, 0e인 바이트 14개를 메시지 끝에 추가해서 블록을 채운다.
나머지 경우들도 비슷하게 처리
복호화 할때는 이렇게 마지막 블록에 01 가 하나있는지 02 가 두개 있는지 03 이 세개 있는지 0f 가 15개 있는지 파악하고 02 03 04 이런식이면 복호화를 거부한다.
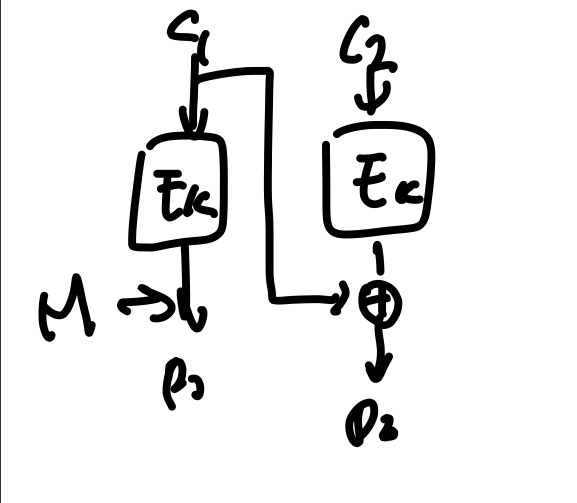
2) 암호문 훔치기
1) 보다 복잡하다.
- 평문 비트 가능
- 같은 길이(암호문,평문)
- CBC에 잘 통하는 채움 오라클 공격에 취약하지 않음
-> 마지막 불완전한 평문 블록에 이전 암호블록비트 붙여서 암호화 -> 평문에 추가하지 않았던 비트들로 구성
P3을 이전 블록의 마지막 비트들과 XOR 해서 암호화 -> C2
이전 블록의 처음 비트들이 C3
-> 비트 길이 유지
문제점은 딱히 없으나 우아하지 않고 제대로 구현하기가 어렵다.
3) 카운터 모드(CTR)
암호화의 장점은 유지하고 단점은 피한다.
블록 암호보다는 스트림 암호에 가깝다.

N는 일회용 토큰값이다.
한 메세지의 모든 블록은 같은 논스 값이지만 두 메시지는 같은 논스 값이면 안된다.
CBC와 달리 CTR 의 논스는 무작위하지 않아도 된다.
고유하지만 하면 되는데 이유는 다음과 같이 노출 할 수 있기 때문이다.

난수 생성해서 논스 사용 -> 비트 수 길어야함
ex) n 비트 암호화 2^(n/2) 회 수행
-> 같은 논스 등장
즉 짧으면 고유할 논스를 사용하기가 어렵게 된다. 중복되기 때문에 .
특별한 장점은 빠르다는 거다.
문제 발생 요인들
1) 중간 값 일치 공격(meet-in-the-middle,MitM)
2) 3DES의 보안수준은 168 비트 x 112 비트 1) 때문에

3DES
만일 K1 == K2 이면 결국 키 K3 을 이용한 DES 와 동일
2DES, 두 번 안하는 이유는 중간 값 일치 공격 때문
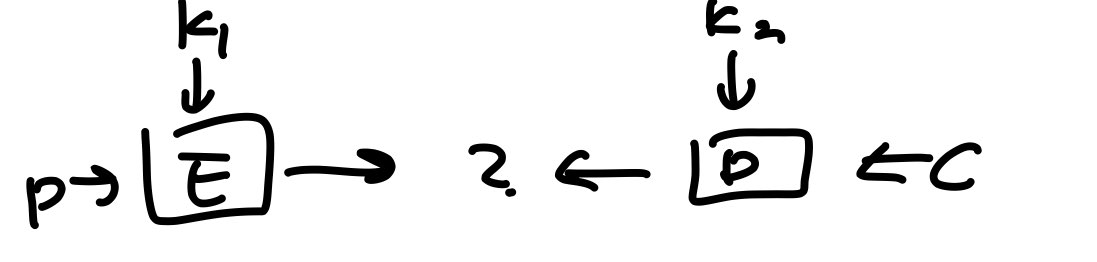
1. 공격자 P, C=E(K2, E(K1,P))
K1,K2는 모르는 56비트
공격자는 2^56개의 E(K1,P) 표를 구축
2. 2^56 K2 값에 대해 D(K2,C) 계산 -> 중간값
3. 색인으로 값 k1 조회
P와 C 통해(K1,K2) 확인
2^57 회의 연산으로 k1,k2 를 복원할 수 있다.
이를 확장하면 3DES 에 대한 공격
K2,K3 모두 가능한 2^112 계산 (보안수준)
채움 오라클 공격(Padding oracle)
대망의 채움 오라클.
CBC모드로 암호화된 암호문 채움이 유효한지에 따라 다르게 행동
성공/오류 돌려주는 블랙박스 또는 API
ex)
공격자 C2 를 복호화
D(k,C2) 를 X 라고 하자
C2 복호화 결과는 P2 이다.
공격자가 무작위로 블록 C1을 선택해서 C1||C2를 오라클에게 보내면 오라클은 C1 XOR P2 = X
끝부분이 유효한 채움(01, 02 두개 , 03 세개) 일때만 성공
이러한 관찰에 기초해서 CBC 암호화에 대한 채움 오라클 공격자는 C2 블록을 다음과 같이 복호화할 수 있다.
C1[0] 은 C1의 첫 바이트라는 의미이다.
블록 C1을 무작위로 선택, 채움 오라클이 유효한 암호문을 받아들일 때까지 마지막 바이트를 변화킴
일반적으로 유효한 암호문에서 C1[15] XOR X[15] = 01 이므로 C1[15] 를 128회 시도하면 X1[15] 를 찾을 수 있다.
-> 오라클 채움 공격에 대해서는 더 많은 이해가 필요할 걸 같다.
이해가 잘 안 간다.
'공부 > 암호학' 카테고리의 다른 글
| 처음 배우는 암호학 ch3 암호학적 보안 (0) | 2020.07.30 |
|---|---|
| 처음 배우는 암호학 ch2 무작위성 (0) | 2020.07.29 |
| 처음 배우는 암호학 ch1 암호화 (0) | 2020.07.29 |

