| 평문 | 암호문 | 암호질의 | 복호질의 | |
| COA | x | o | x | x |
| KPA | o | o | x | x |
| CPA | o | o | o | x |
| CCA | o | o | o | o |
선택된 암호문을 공격하는 모형인 CCA 는 암호가 깨진 게 아니다. 중요한 건 비밀 키를 알아내는 것이다.
보안 목표
= 비구별성(indistinguishability, IND)
평문 p1,p2를 공격자가 암호질의를 수행해도 어떤 평문을 암호화한 것인지 구별할 수 없어야함
= 비가소성(non-malleability,NM)
p1과 c1을 알때 p1과 연관이 있는 p2의 c2를 알 수 없어야한다.
반전(OTP는 알수 있음)
같은 키로 암호화한 평문을 XOR 연산을 통해 알 수 있다.
보안 개념
다음과 같은 형식으로 이루어진다.
-IND-CPA : 선택된 평문에 대한 비구별성
-NM-CCA : 선택된 암호문 공격에 대한 비가소성
IND-CPA(의미론적 보안, semantic security)
: 공격자가 암호문으로 부터 평문에 관한 어떤 정보도 알아낼 수 없음.
만족시키기 위해서는 같은 평문을 두번 암호화 했을 때 'C1 != C2' 해야함.
달성하기 위한 간단한 구축 방법
-결정론적 비트 발생기(DRBG) 사용
-> 주어진 비밀 값에 기초해서 무작위로 보이는 비트열을 생성하는 알고리즘
E(K,R,P) = (DRBG(K||R) XOR P, R)
R은 암호화 수행할 때마다 새롭게 무작위로 선택되는 비트
K||R은 이어붙은 비트열
DRBG 가 실제로 무작위 비트열 생성한다고 가정
IND-CPA 보안 증명하기 위해 귀류법 사용
1. 암호문은 무작위 비트열로 부터 구별( 가정)
1이 참이면
2. DRBG(K||R) XOR P 무작위 비트열로부터 구별
CPA 에 의해서 XOR R 을 한번 더 함
3. DRBG(K||R) 을 무작위 비트열로부터 구별
무작위 비트열을 생성한다는 것을 DRBG(K||R) 을 무작위 비트열로부터 구분할 수 없다는 가정과 모순
즉 공격자가 암호문으로 부터 비트열을 구분 못한다는 의미는 이 암호가 안전하다는 의미이다.
보안 개념들 함의 관계
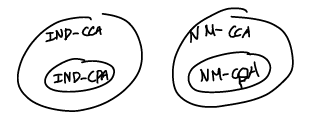
CPA 가 가능한거는 CCA 도 가능하다.
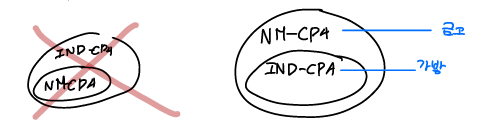
비대칭 암호화은 핵심은 개인키를 알고 있으면 공개키 계산이 가능하지만 공개키만 알고 있을 때는 개인키 계산이 불가능한 것이다.
공격자가 암호화 질의를 하는 CPA 는 늘 공개키로 질의를 하는 거다.
- 인증 암호화(Authenticated Encryption, AE)
대칭 암호화 일종
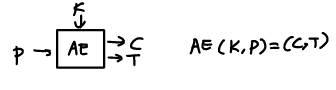
ex) 메시지에 카운터 번호 포함시키는 방법
무결성(integrity) 보장
-> 중간에 공격자가 가로챌 경우 카운터가 올라감으로 누가 복호화 했다는 사실을 알 수 있다.
- AEAD(Authenticated Encryption with Associated Data)

K 뿐만 아니라 암호화가 되지 않는 어떤 자료를 함께 넣어준다.
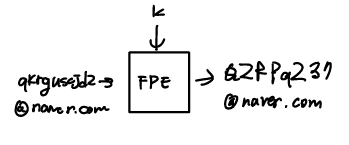
- 형태 보존 암호화(Format-Preserving Encryption, FPE)
IP 주소를 암호화하면 IP 주소가 나오고 이런 식으로 형식을 지켜주는 암호화 방법
- 완전 준동형 암호화(Fully Homomorpyhic Encryption, FHE)
암호학자들의 성배와 같은 방식인데 이는 암호문을 복호화 과정없이 다른 암호문으로 암호화하는 방식이다.
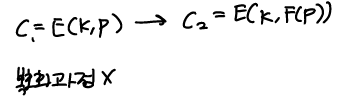
2009년도에 고려된 방식인데 느리다는 단점 때문에 제대로 사용되지 못하고 있다.
- 검색 가능 암호화(Searchable Encryption)
검색 질의 자체를 암호화한다. 가능한지의 여부를 아직 모르는 실험적인 암호화 방식이다.
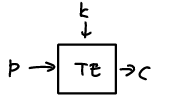
- 조율 가능 암호화(Tweakable Encryption,TE)
조율값(Tweak) 존재
같은 제품 사용 고객이 다른 고객을 해킹하는 것을 방지한다.
디스크 암호화가 핵심 -> 블록이나 섹터 번호를 조율값으로 사용한다.
이 이외에도 특성기반 암호화, 방송 암호화, 함수 암호화, 식별자 기반 암호화, 메시지 잠금 암오화, 프록시 재암호화 등이 있다.
'공부 > 암호학' 카테고리의 다른 글
| 처음 배우는 암호학 ch4 블록암호 (0) | 2020.08.05 |
|---|---|
| 처음 배우는 암호학 ch3 암호학적 보안 (0) | 2020.07.30 |
| 처음 배우는 암호학 ch2 무작위성 (0) | 2020.07.29 |

