※이 글은 나동빈님 포스팅을 보고 복습용으로 제작이 되었습니다.
https://blog.naver.com/ndb796/221237111220
27. 네트워크 플로우(Network Flow)
네트워크 플로우(Network Flow)는 특정한 지점에서 다른 지점으로 데이터가 얼마나 많이 흐르고 있는가를...
blog.naver.com
안녕하세요. 옆집 컴공생입니다. 오늘은 네트워크 플로우(Network Flow) 에 대해 배워 볼거에요. 그전에 구현에서 BFS 를 써서 구현을 하기 때문에 개념을 복습하는 게 좋을 거 같습니다 .
https://com24everyday.tistory.com/109?category=1123820
너비 우선 탐색(BFS)
※이 포스팅은 나동빈님 강의를 듣고 정리한 것 입니다.※ https://www.youtube.com/watch?v=66ZKz-FktXo&list=PLRx0vPvlEmdDHxCvAQS1_6XV4deOwfVrz&index=16 너비 우선 탐색 (Breath-First-Search, BFS)입니다...
com24everyday.tistory.com
네트워크 플로우는 특정 지점에서 다른 지점을 데이터가 얼마나 흘러갈 수 있냐를 측정하는 알고리즘입니다. 이러한 알고리즘은 교통체증, 네트워크 데이터 전송 등의 다양한 분야에 활용되어지고 있습니다. 다음 예시로 개념을 알아보겠습니다.
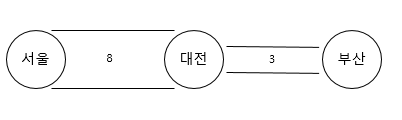
서울에서 대전을 가는데 도로의 폭이 8입니다. 그리고 대전에서 부산을 가는데 도로의 폭이 3 입니다. 이럴때 1초만에 이 도로를 건널 수 있다 가정했을때 8명을 보내면 1초 뒤에 결과는 다음과 같이 됩니다.
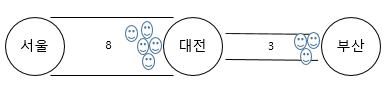
도로 폭이 3이기 때문에 8 명중에 3명 만이 도로를 통과 한 겁니다.
애초에 대전에 머무는 인원이 없이 모두 부산에 도착할 수 있게 할려면 서울에서 몇 명을 보냈어야할까요?

1초마다 3명을 보내야 아무도 대전에 머물지 않습니다. 이런 경우 3/8 , 3/3 로 표현 했습니다. 표현 방식은 유량/용량입니다. 유량(Flow)은 현재 흐르고 있는 양이고 용량(Capacity)은 흐를 수 있는 양입니다. 즉 서울에서 대전으로 가는 도로는 8명이 갈 수 있는 길이지만 현재 3명이 갔다는 뜻입니다.

위 그래프에 용량을 보면서 1에서 4까지 가장 많은 유량을 보내려고 할 때 가장 합리적인 양은 얼마일까요?
네. 다음과 같을 겁니다.

눈치채셨겠지만 가장 적은 용량을 보내야 위의 '서울 -> 부산' 예시처럼 정체 현상이 발생하지 않으면 가장 많은 양을 보낼 수 있습니다. 이러한 문제를 해결하는 핵심 알고리즘이 네트워크 플로우 알고리즘입니다. 일반적으로 최대 유량(Max Flow)문제라고 정의합니다.
최대 유량 문제는 각 간선에 정해진 유량이 있을 때 A에서 B로 최대로 보낼 수 있는 유량의 크기를 구하는 문제입니다.
이제 좀 더 많은 간선과 노드 그래프를 살펴봅시다.
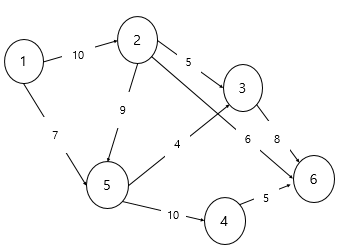
1부터 6까지 흘려보낼 수 있는 최대 유량은 얼마나 될까요? 기본적으로 최대 유량 문제는 단순하게 가능한 모든 경우의 수를 탐색하는 방법을 사용합니다. 이때 BFS(너비 우선 탐색)을 이용하는 것이 일반적입니다. 이를 에드몬드 카프(Edmonds-Karp) 알고리즘이라고 합니다.
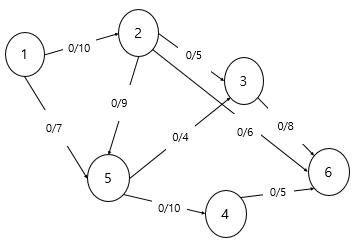
가능한 모든 수를 탐색해야하기 때문에 현재 유량(Flow)을 0으로 설정합니다. 이후 용량(Capacity) 안에서 가능한 용량의 양을 반복적으로 더해주면 됩니다.
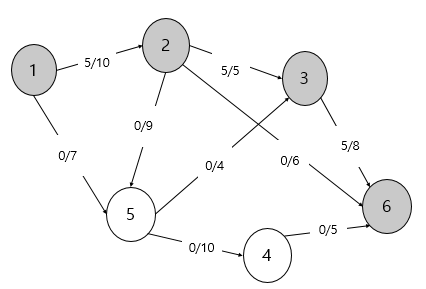
먼저 ' 1-> 2 -> 3 -> 6' 으로 가는 길을 살펴봅시다. 최소 유량이 5인걸 할 수 있습니다. 5만큼 6으로 흘려보내줍니다. 그래서 다음 간선 들에 모두 5가 더해진 것을 볼 수 있습니다.

다음은 '1 -> 2 -> 6' 으로 갔을 땐 최대 1 -> 2 가 5를 넣는게 최대 유량입니다. 그러므로 간선마다 5을 더해줍니다.
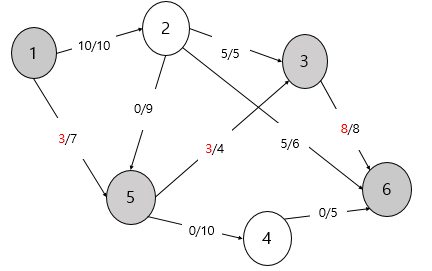
다음은 '1 -> 5 -> 3 -> 6' 로 보내보겠습니니다. '3->6' 이 최대 유량이 3이기 때문에 각 간선마다 3을 더해줍니다.
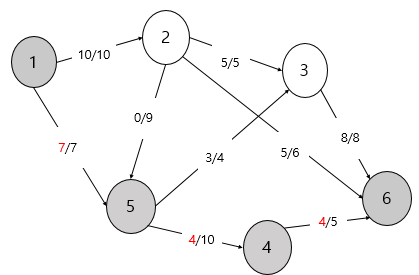
다음은 '1 -> 5 -> 4 -> 6' 로 보내보겠습니니다. '1->5' 이 최대 유량이 4이기 때문에 각 간선마다 4을 더해줍니다.
이러면 모든 경우를 끝낸거 같습니다.
▷근데 아직 끝난게 아닙니다. 여기서 네트워크 플로우의 핵심 개념이 나오는데요. 바로 '음의 유량' 입니다. 최대 유량 알고리즘은 모든 가능한 경로를 다 계산해주기 위해 음의 유량도 다 계산해줍니다. 말 그대로 양이었던 과정에서 반대로 가는 유량이 존재한다고 생각하면 됩니다. 다음 사진과 같은 겁니다.
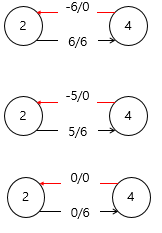
첫번째 그림은 보면 2에서 4까지 6이 흐르고 있다고 생각할 수 있습니다. 하지만 반대로 4에서 2까지 -6이 흐르고 있다고 볼 수도 있는겁니다. 실제로 음의 유량은 불가능합니다. 그러면 왜 이런 거까지 나누어주어야하나. 그건 '남아있는 모든 가능한 경로를 더 찾아내기 위함' 입니다. 이런 식으로 음의 간선을 포함시키면 새로운 경로를 찾을 수 있습니다.
제가 그렸던 그래프에는 예시를 못찾아서 살짝 숫자를 바꿨습니다.
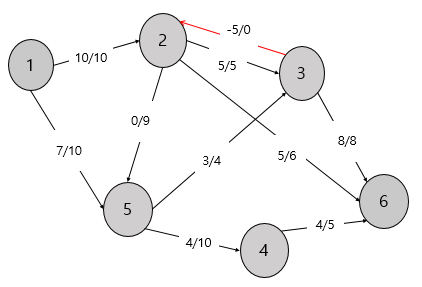
이렇게 2와 3에 음의 간선이 있습니다. 다음과 같은 새로운 경로를 찾을 수 있습니다.

'1 -> 5 -> 3 -> 2 -> 5 -> 4 -> 6' 로 새로운 1만큼의 유량을 더 보낼 수 있습니다. 여기서 주의 해야할 것은 2 -> 3으로 가는 유량은 하나 빼주어야한다는 겁니다.
이처럼 바꾼 그래프에서 최대 유량이 18을 알 수 있습니다.
최대 유량 알고리즘은 또 순서가 상관이 없습니다. 남아있는 양이 1이 넘으면 계속해서 흘려 보내주면 알아서 최적화가 이루어진다는 점에서 굳이 유량을 보내는 순서를 고려할 필요가 없습니다.
기본적으로 BFS를 사용해서 모든 가능한 경로를 다 찾아서 남아있는 용량만큼 유량을 흘려 보내주는 것을 반복함녀 됩니다.
에드몬드 카드 알고리즘의 경우 시간복잡도가 O(VE^2) 입니다.
'공부 > 알고리즘' 카테고리의 다른 글
| 기말 Greedy_approach 정리 (0) | 2020.06.24 |
|---|---|
| Knapsack Problem(배낭 문제) (0) | 2020.06.21 |
| 강한 결합 요소(Strongly Connected Component) (0) | 2020.06.13 |
| 위상정렬(Topology Sort) (0) | 2020.06.12 |
| 플로이드와샬 알고리즘(FloydWarShall) (0) | 2020.06.11 |



