※다음 포스팅은 나동빈님 블로그를 보고 포스팅한 것입니다.
https://blog.naver.com/ndb796/221236952158
26. 강한 결합 요소(Strongly Connected Component)
강한 결합 요소란 그래프 안에서 '강하게 결합된 정점 집합'을 의미합니다. 서로 긴밀하게 연결되어 있다고...
blog.naver.com

강한 결합 요소란 그래프 안에서 '강하게 결합된 노드의 정점 집합' 라는 의미 입니다. 서로 강하게 연결되어 있다고 하여 강한 결합 요소입니다. 이는 SCC 알고리즘이라고 불리는 데요. SCC 는 '같은 SCC 에서 선택한 두 정점은 서로에게 도달이 가능하다' 는 특징이 있습니다.
다음 그래프에서 SCC 를 구하면 다음과 같습니다. 집합에 속하는 정점끼리 서로 도착이 가능하면 SCC입니다.
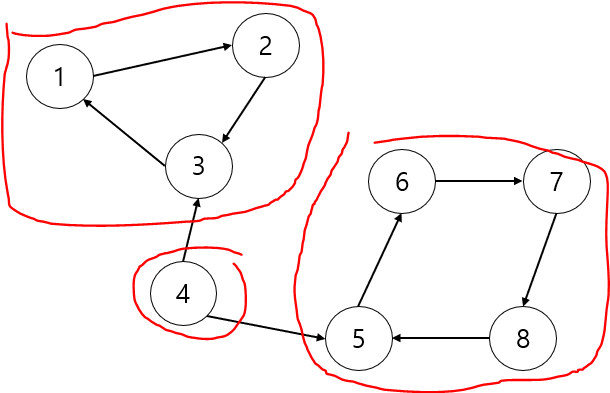
총 3개의 집합이 만들어졌는데 보면 각 집합에 점접들끼리 순회가 가능합니다. 가장 왼쪽에 있는 집합에서는
'1 -> 2', '1 -> 3'
'2 -> 1', '2 -> 3'
'3 -> 1', '3 ->2'
이 다 가능합니다.
기본적으로 사이클이 발생한다면 무조건 SCC입니다. 또한 무향 그래프라면 전체가 SCC가 되기 때문에 SCC 알고리즘은 방향 그래프일때만 의미가 있습니다.
SCC 알고리즘을 추출하는 대표적인 알고리즘은 1) 코사리주 알고리즘(Kosaraju's Algorithm) 과 2) 타잔 알고리즘(Tarjan's Algorithm)이 있습니다. 일반적으로 코라사주 알고리즘 구현이 쉽지만 타잔 알고리즘이 적용이 더 쉽다고 합니다. 그러니 저희도 타잔 알고리즘에 대해 배워보겠습니다.
타잔 알고리즘은 '모든 정점에 대해 DFS(Depth-first Search) 을 수행하며 SCC를 찾는 알고리즘'입니다.
간단한 그래프로 예제를 들며 확인해보겠습니다.
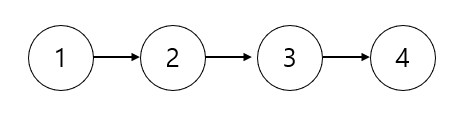
이 그래프는 한 번 나아가면 돌아올 수가 없기 때문에 SCC 라고 할 수 가 없습니다. 다음 그래프가 SCC 가 될려면 어떻게 해야할까요? 단 한 엣지만 더 그으면 됩니다. 다음과 같이 하면 SCC로 모든 정점들이 서로에게 도달 가능합니다.

2에서 4까지 SCC가 되게 할려면 다음과 같이 이으면 되겠죠.
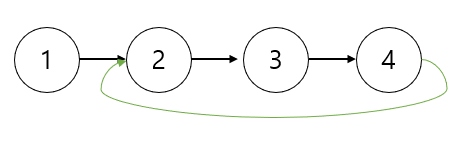
즉 부모 노드로 돌아올 수 있어야 SCC가 성립될 수 있다는 걸 알 수 있습니다. 이를 통해 부모에서 자식으로 나아가는 알고리즘으로 DFS 알고리즘이 사용이 됩니다.
https://com24everyday.tistory.com/110?category=1123820
깊이 우선 탐색(DFS)
※이 글은 나동빈님의 유튜브를 보고 복습용으로 포스팅됩니다※ https://blog.naver.com/ndb796/221230945092 16. 깊이 우선 탐색(DFS) 깊이 우선 탐색(Depth First Search)은 탐색을 함에 있어서 보다 깊은 것을..
com24everyday.tistory.com
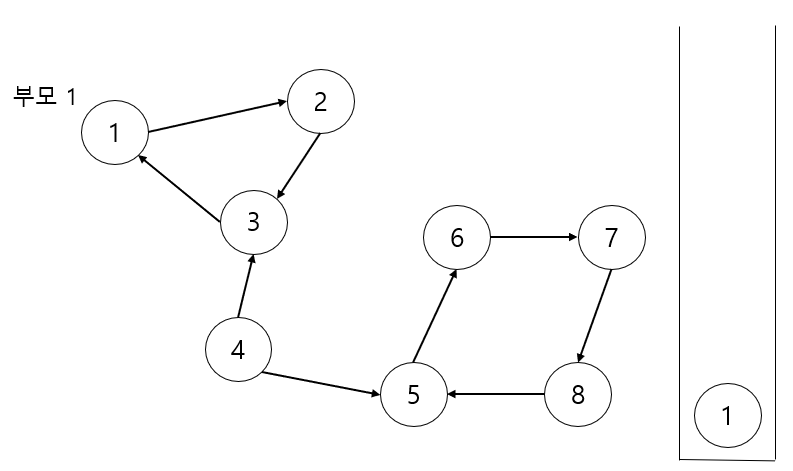
첫번째로는 정점 1을 기준으로 DFS를 수행합니다. 그리고 또 다른 정점을 기준으로 DFS를 수행하게 됩니다. 일종의 재귀함수같이 말이죠. 일단 기본적으로 스택을 사용할때는 재귀함수로 구현도 가능합니다. 컴퓨터의 구조상 스택 구조로 이루어지기 때문입니다. 노드 1이 스택에 들어가고 부모는 자기 자신으로 1입니다.
이제 1과 연결된 노드 2를 스택에 넣습니다. 부모는 자기 자신으로 2입니다.
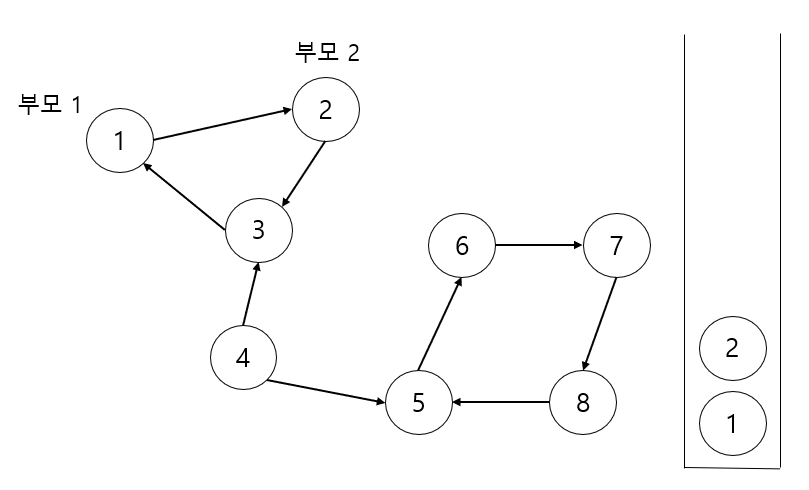
노드 2와 연결된 노드3 을 스택에 넣어줍니다. 부모는 역시 자기 자신입니다.
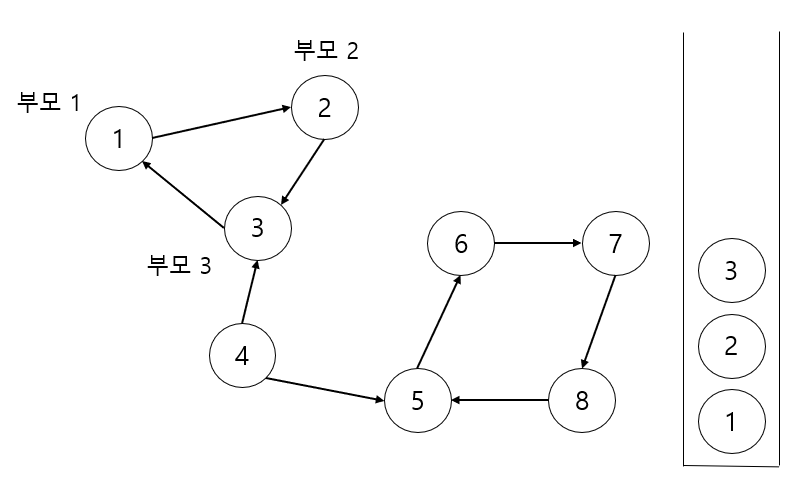
이제 노드 3을 기준을 DFS를 수행할땐 연결된 1을 확인하게 되는데 이때 1의 DFS가 진행되고 있음으로( 스택에 들어 있음으로) 정점 3은 '나의 부모가 1이구나'를 알게 됩니다. 이렇게 되는 순간 3의 부모는 1로 변하고 DFS 를 끝냅니다. 노드2도 차례대로 부모를 1로 갱신하고 DFS 함수를 끝냅니다.
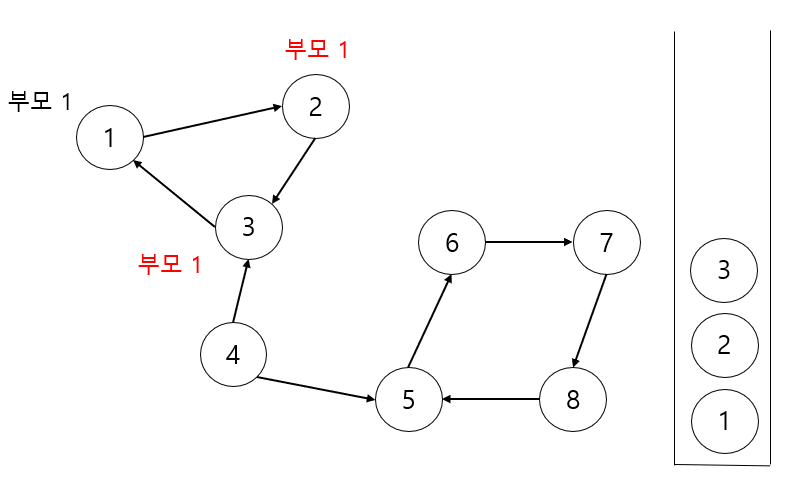
여기서 노드 1 은 DFS 함수를 끝내는데 자기 자신이 부모라는 걸 깨닫고 'SCC의 부모에 해당하네' 라고 파악하고 자기 자신이 나올때 까지 스택을 뽑아내게 됩니다. 결과적으로 노드 1, 노드2, 노드3 이 스택에서 나오고 SCC그룹을 발견하게 됩니다.
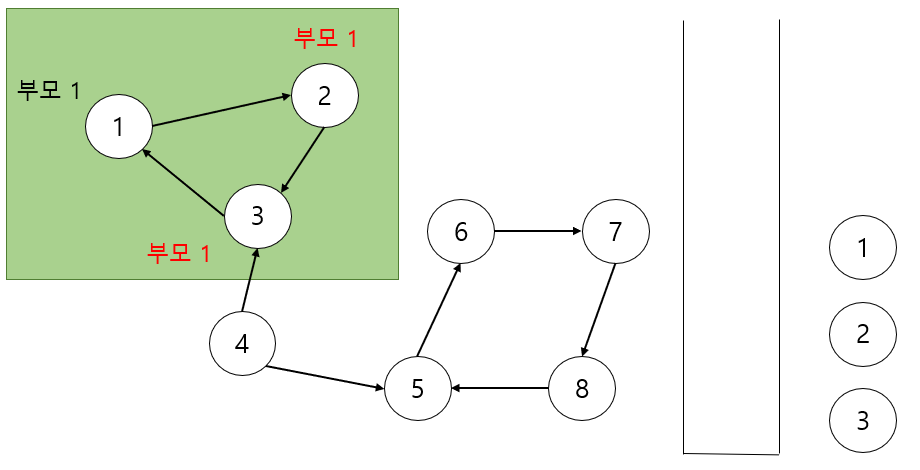
그리고 아직 방문하지 않은 정점 4에서부터 DFS를 수행합니다. 노드 4부터 노드 8까지 차례대로 스택에 들어가게 됩니다.

다음과 같아집니다. 그리고 노드 8이 노드 5를 가리킬때 노드가 아직 DFS 함수를 진행 중 임으로 '내 부모가 5이구나!'를 알게됩니다. 그렇게 노드 8을 시작으로 7 ,6 의 DFS 함수가 끝나고 부모가 5로 갱신됩니다.
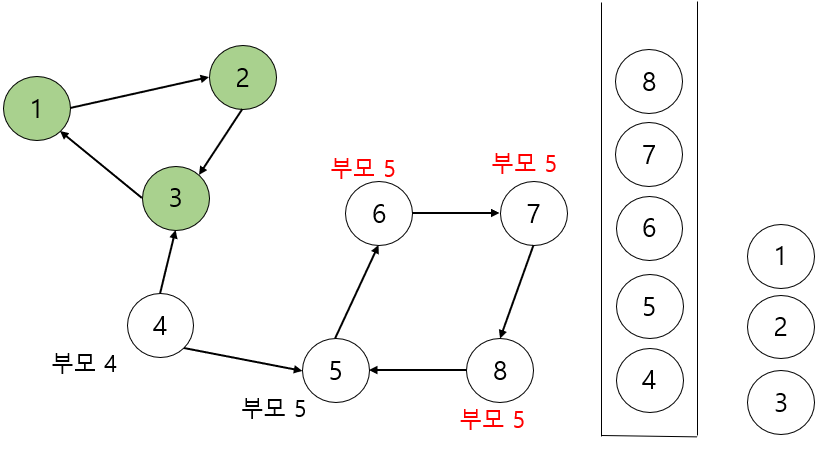
여기서 5는 dfs 함수를 끝내면서 자기 자신이 '내가 SCC의 부모이구나' 라는 걸 파악하고 스택에서 자기자신이 나올때 까지 뽑아내게 됩니다.
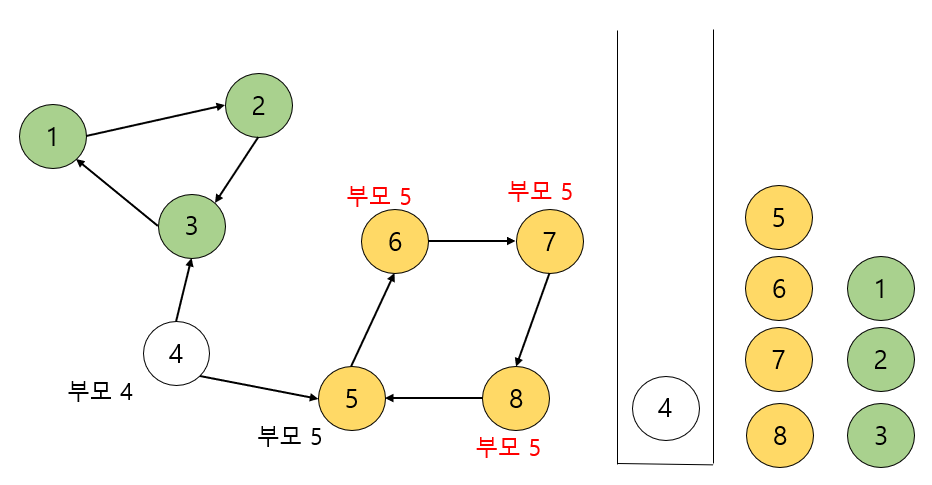
노드 4도 DFS 함수가 끝나면서 스스로가 부모임을 깨닫고 자기 자신을 만날 때까지 4를 스택에서 뽑아내게 됩니다.
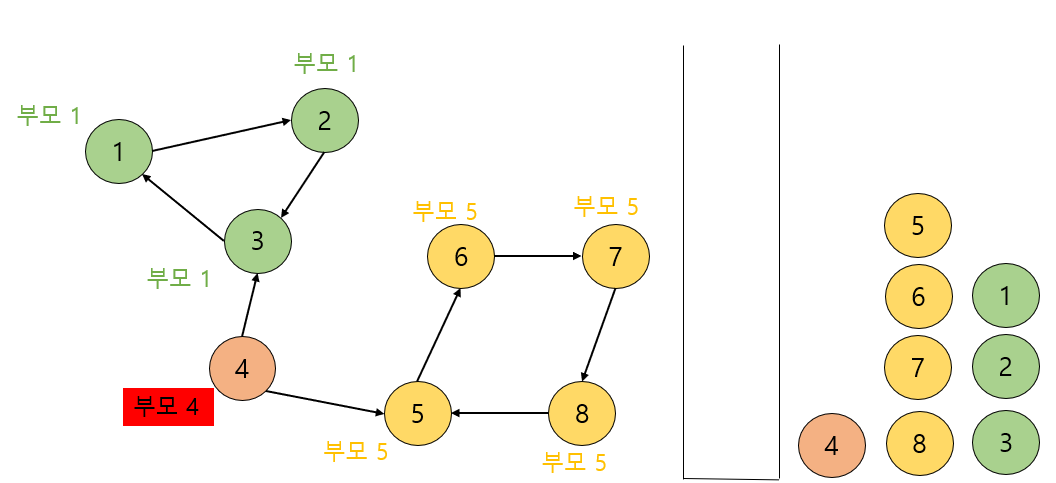
위와 같은 SCC 3개를 다 구했습니다. 이렇게 SCC 알고리즘을 구현에 봤습니다.
C++로 구현해보겠습니다.
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
#define MAX 10001
using namespace std;
int id = 0, d[MAX];//각 노드마다 고유한 번호 할당
bool finished[MAX];//현재 특정 노드에 대한 DFS 가 끝났는지 판단
vector<int> a[MAX];
vector<vector<int> > SCC;
stack<int> s;
//DFS는 총 정점의 갯수만큼 실행됩니다.
int dfs(int x) {
d[x] = ++id;//노드마다 코유한 번호 할당
s.push(x); //스택에 자기 자신을 삽입
int parent = d[x]; //자신의 부모가 누구인지 확인, 처음에는 자기 자신
for (int i = 0; i < a[x].size(); i++) {
int y = a[x][i];//인접한 노드 자체를 가리키기
if (d[y] == 0) parent = min(parent, dfs(y)); //만약 해당노드를 반복한 적이 없다면 해당 노드로 dfs 수행
//여기서는 3의 노드가 1보다 작기 때문에 1을 부모노드로 정한다.
else if (!finished[y]) parent = min(parent, d[y]); //처리 중인 이웃
}
//부모노드가 자기자신인 경우
if (parent == d[x]) {
vector<int> scc;
while (1) {
int t = s.top();
s.pop();
scc.push_back(t);
finished[t] = true;
if (t == x) break;
}
SCC.push_back(scc);
}
return parent;//자신의 부모 값 반환
}
int main()
{
int v = 8;
a[1].push_back(2);
a[2].push_back(3);
a[3].push_back(1);
a[4].push_back(3);
a[4].push_back(5);
a[5].push_back(6);
a[6].push_back(7);
a[7].push_back(8);
a[8].push_back(5);
for (int i = 1; i <= v; i++) {
if (d[i] == 0) dfs(i);
}
printf("SCC의 갯수 : %d\n", SCC.size());
for (int i = 0; i < SCC.size(); i++) {
printf("%d번째 SCC:", i + 1);
for (int j = 0; j < SCC[i].size(); j++) {
printf("%d ", SCC[i][j]);
}
printf("\n");
}
}

오늘은 이렇게 강한 결합 요소에 대해 배워보았습니다. 이 자체로는 별 의미가 없고 위상 정렬과 함께 쓰일 때 의미가 크다고 합니다. 그래도 알고리즘 대회를 준비하시는 분들께는 꼭 필요한 내용입니다.
https://com24everyday.tistory.com/145
위상정렬(Topology Sort)
위상 정렬(Topology Sort) 는 순서가 정해져있는 작업을 차례로 수행할 때 순서를 결정해주기 위해 사용되는 알고리즘입니다. 예시를 바로 볼까요. 다음과 같이 할 일 루틴이 있다고 합시다. 청소나
com24everyday.tistory.com
수고하셨습니다.
'공부 > 알고리즘' 카테고리의 다른 글
| Knapsack Problem(배낭 문제) (0) | 2020.06.21 |
|---|---|
| 네트워크 플로우(Network Flow) (0) | 2020.06.15 |
| 위상정렬(Topology Sort) (0) | 2020.06.12 |
| 플로이드와샬 알고리즘(FloydWarShall) (0) | 2020.06.11 |
| 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2020.06.10 |



