강의는 모두를 위한 머신러닝이다.
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io
Lecture1. 머신러닝 기초
- ML이란?
- Learning 이란?
- regression 이란?
- classification 이란?
머신러닝이란?
- 프로그래밍으로는 하기 어려운 동작을 해결하기 위해 1959년 Arthur Samuel 에 의해 탄생
학습이란?
Supervised/ UnSupervised 로 나뉘어지는데 Supervised 는 학습 데이터셋이 이미 label 되어 있는 것이다.
예를 들면 강아지/고양이/원숭이 사진이 각각 100개씩 이미 레이블화가 되어 있다는 거다.
아래의 그림을 통해 제대로 살펴볼 수 있다.

반대로 Unsupervised learning 은 un-label 데이터다. 구글 뉴스를 그룹핑한다든지 단어군집화 등이 이 분류에 속한다.
Supervised learning 유형
Supervised learning에는 세가지 유형이 있다.
-Regression(회귀)
0~100점처럼 연속적인 형태의 분류
-Binary Classification
T/F 처럼 이진적인 분류
-Multi-label Classification
학점 A,B,C,D,F 처럼 여러개의 레이블 분류
Lecture2. 선형 회귀
- Regression
- Hypothesis
- Cost function
- Regression
목표는 x 값을 넣었을 때 적절한 y 값을 내는 것.
위에서 언급했듯이 연속적인 데이터가 존재.
예를 들어 이 데이터셋을 학습시킨 모델에 x = 4 를 넣게 되면 값은 4가 나와야 잘 학습되었다고 말할 수 있을 것이다.
| x | y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
-Hypothesis
(Linear)Hypothesis는 가설, 위와 같이 데이터를 기반으로 만든 그래프에 선형 그래프를 예측한다.
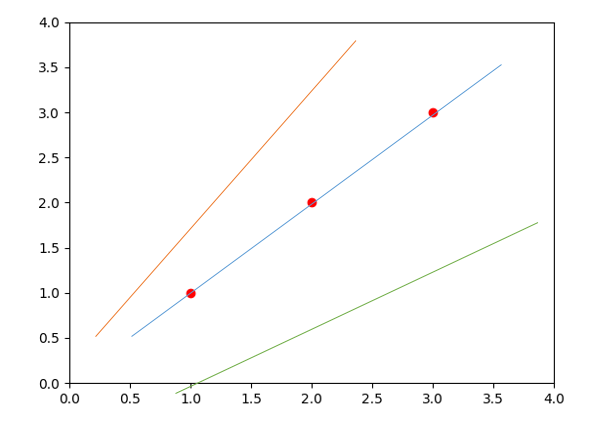
여러 그래프를 예측할 수 있지만 최대한 맞는 (파란색 선) Hypothesis function H(x) 를 찾는 것이 목표이다. 여기서 H(x) 는 일차 함수로 H(x) = Wx + b 로 나타낼 수 있기 때문에 적절한 W, b 를 찾는다고 이야기할 수 있다.
그럼 '최대한 맞는'은 어떻게 파악할 수 있는 걸까?
이는 Cost function(=Loss function) 으로 알 수 있다.
-Cost function
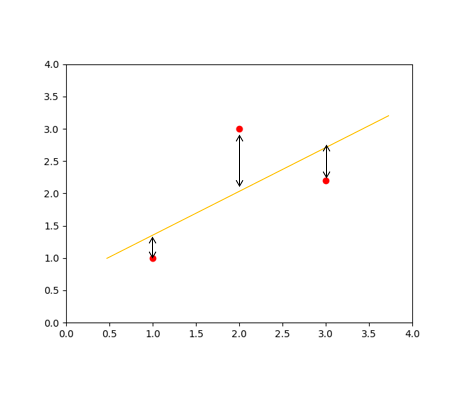
직관적으로 생각해보면 예측한 H(x) 과 데이터셋과의 차이를 비교하면 될 것이다.
여기서는 2차원이기 때문에 다음과 같은 수식으로 정리될 수 있다.
제곱을 한 이유는 거리의 차가 음수 양수로 존재할 수 있기 때문이다.
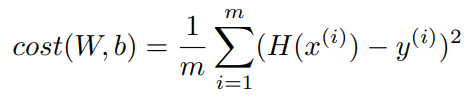
위 수식과 같이 로스 함수 정의할 수 있다. H(x) 함수와 실제 데이터셋과의 차이의 평균이다.
이를 최소화하는 것이 우리의 목표로고 할 수 있다. 좀 더 formal 하게 쓰자면 아래와 같다.
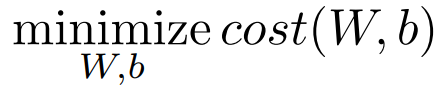
이렇게 regression의 간단한 개념과 Hypothesis와 cost function(=loss function) 에 대해 알아보았다.
Lecture3 - Cost 최소화 하기
목표는 Cost function을 최소화 시키는 건데 어떻게 최소화시킬까? 에 대해 알아보자.
그래프를 간단히 하기 위해 위에서 만들었던 H(x) 에 y절편에 해당되는 b 를 날려버리자.
그럼 아래와 같은 간단한 수식으로 정리된다.
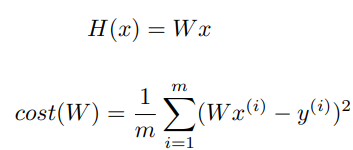
W에 0,1,2,라는 값을 넣어서 계산을 하면 아래와 같은 계산이 된다. cost(W) 함수에 W를 대입하면 쉽게 구할 수 있다.
W =1 cost(W) = 0
W =0 cost(W) = 4.67
W =2 cost(W) = 4.67

이와 같이 W에 값을 변경하면서 x축이 W 고 y축이 cost 인 그래프를 그리면 다음과 같이 2차 함수 같은 그래프가 그려진다.
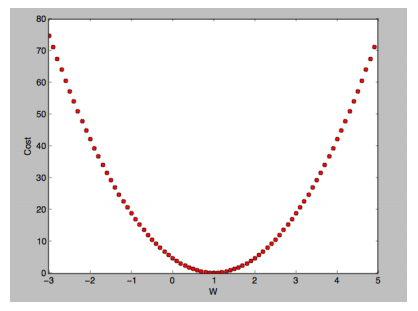
우리의 목표와 부합하는 값은 W = 1에 해당하는 값이다. 이를 구할려면 어떻게 해야할까?
Gradient descent algorithm 을 사용할 것이다.
-Gradient descent algorithm
이는 cost function 을 최소화하기 위해 자주 사용되는 알고리즘이다.
또 기울기를 계속 타고 내려가면 가장 낮은 곳에 도착하지 않을까라는 생각을 기반으로 만들어진 알고리즘이다.
알고리즘 이름 그대로 기울기를 타고 내려간다고 생각하면 된다.

기울기는 미분을 통해 구할 수 있다. 여기서는 다음과 같은 식이 나올 것이다.
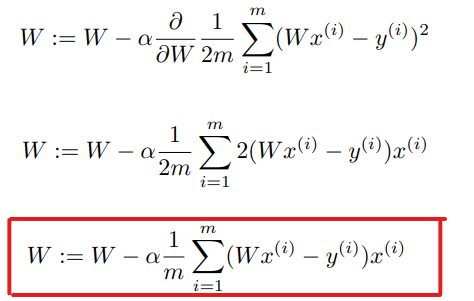
이렇게 Gradient descent 알고리즘을 통해 최적의 W 값을 구할 수 있다.
하지만 고려해야할 사항이 있다. 만약 cost function 에 대한 그래프를 그렸는데 다음과 같이 그려지면 어떨까?
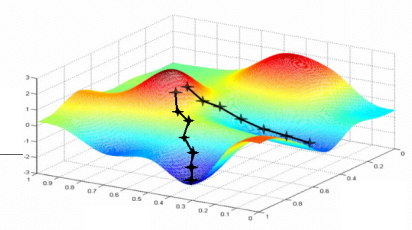
위 그래프와 같다면 어디에서 출발했는지에 따라 W 의 값이 달라진다. 이를 local minimum problem이라고 한다. 최적 값이 아닌데 최적값이라고 착각할 수 있는 상황을 의미한다. 이를 해결하고자 하는 알고리즘 또한 많다. (오늘은 언급하지 않는다)
그러므로 Gredient descent 알고리즘 사용할 때는 Cost function 그래프가 아래 사진과 같은 Convex function(볼록함수)인지를 확인해야한다.
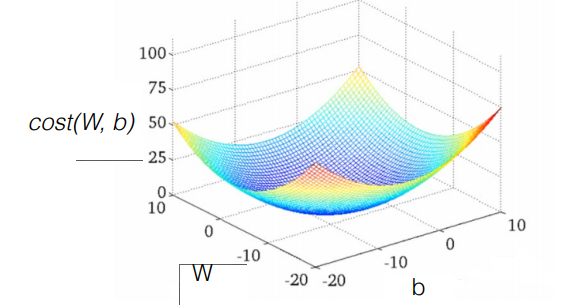
수식 출처 :www.holehouse.org/mlclass/
Machine Learning - complete course notes
Stanford Machine Learning The following notes represent a complete, stand alone interpretation of Stanford's machine learning course presented by Professor Andrew Ng and originally posted on the ml-class.org website during the fall 2011 semester. The topic
www.holehouse.org
세미나 후 질문
1. 이미 분포도를 그릴 수 있으면 Gradient Descent Algorithm 을 그릴 필요가 없지 않냐?
: 잘못 알고 있었던 개념이었다.
저런 분포도에 그래프면 Gradient Descent Algorithm 으로 적절한 W 를 구할 수 있는 거다.
2. Cost function 양수와 음수 때문에 제곱을 한다고 이야기 했는데 절댓값을 씌우면 되지 않나?
: 제곱을 했을 때 미분 값을 구하는 게 편해져서 그런거였다.
'스터디 > 인공지능 논문 읽기' 카테고리의 다른 글
| 논문 요약하기 : Zeroth Order Optimization (ZOO) (0) | 2020.11.20 |
|---|---|
| [논문읽기스터디]1.Adversarial Attack 개요 (0) | 2020.10.28 |
