Fermat's Theorem/페르마의 정리

안녕하세요. 오늘은 Fermat's Theorem 에 대해 알아보도록 하겠습니다. 

만약 p가 Prime Number 일 때 (소수) , gcd(a,p)=1->서로소 일 때  a^(p-1) = 1 ( mod p )  a^p = a( mod p )

Fermat's Theorem 은 public key 와 primality testing 에 유용하다 .

 

 

테이블을 잘 보면 a 의 숫자에 따라 반복되는 숫자들이 있다.

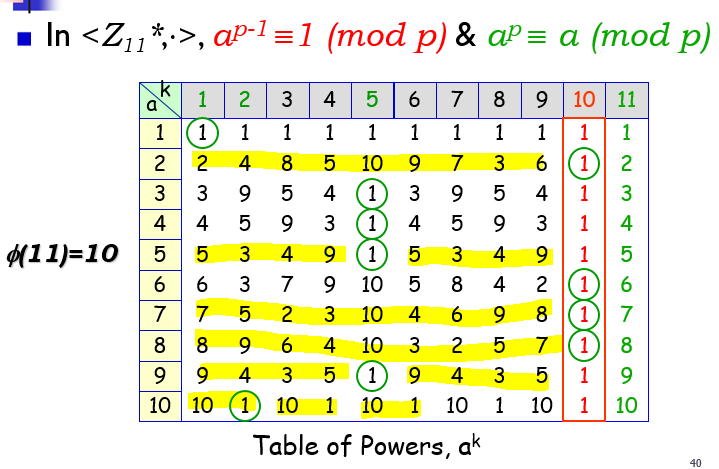
2,6,7,8 등은 2부터 10 까지 

3,4,5,9 는 4개의 숫자가 반복된다. 10은 10,1 에서 반복되는 것을 볼 수 있다. 

 

이렇게 전체를 Generator 하는 수는 (여기선 2,6,7,8)

의 수와 동일하다.

 

Fermat's Theorem 증명

Proof of a^(p-1) ( mod p ), gcd(a,p) =1    1. p보다 작은 양수 집합을 생각해보자. S = {1,2,3,...., p-1}   이중에 한 수를 무작위로 선택하여 'a' 라고 지정하자.  2. 그리고 위 set 에 a를 곱하자.    S x a = {a,2a,3a,...., a(p-1)}   3. 이 식에 modular p를 한다.    X = { a mod p, 2a mod p, .. (p-1)a mod p }   p와 a 가 서로소이기 때문에 위에 연산에서 0인 원소는 존재하지 않는다.      ja = ka (mod p) , where 1<=j<k<=p-1 라고 가정 하자.  gcd(a,p) =1 이기 때문에  j = k(mod p) 이다.  하지만 이러면 초기 비교식과 일치하지 않으므로 모순인 걸 알 수 있다.   결국 S 와 X 의 원소가 동일 함을 볼 수 있다.  그렇기 때문에 이러한 결론도 도출해 낼 수 있다.    a x 2a x ... x (p-1)a = [(1x2x...x(p-1)] ( mod p ) a^(p-1) x ( p -1)! = (p-1)! ( mod p ) 즉 a^(p-1) = 1 ( mod p )