오늘은 간단하게 정리를 해보고자 합니다.
파노라마를 만들기 위해서는 이미지가 이동, 회전, 크기 변화 등등을 걸쳐야합니다.
오늘은 그걸 하게 해주는 Transformation 들의 종류를 알아볼 것입니다.
그전에 Image Warping(와핑) 에 대해서도 배워보고 넘어가도록 합시다.
Image Warping
이미지 필터링은 이미지의 범위, 즉 y축 값을 변화시키는 거고 (색 변화 등)
이미지 와핑은 이미지의 도메인, 즉 x 축 값이 변화시키는 겁니다. (위치 변환만)
정리하자면 이미지 필터링과 이미지 와핑에 차이는 위치 변화 유무입니다.

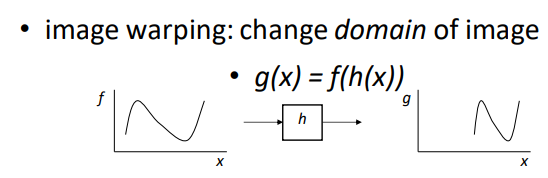
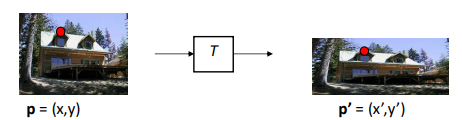
Parametric (global) warping
파라미터로 이 과정을 표현 가능하고 특정 포인트만 변하는 것이 아니라 이미지 전체가 변하기 때문에 global 입니다.
이 파라메티릭 와핑에 종류는 다음과 같습니다.

이런 와핑은 변환 함수를 통해서 새로운 값을 냅니다.
아래 행렬 계산을 보면 이러한 계산들이 linear transform이라는 걸 알 수 있습니다.
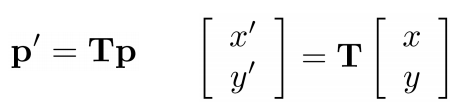
흔한 linear transform의 예는 다음과 같은 scale 변화와 회전등을 뽑을 수 있습니다.
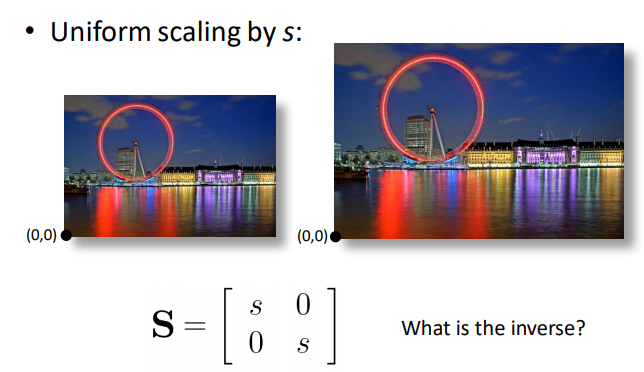
P' = Tp 계산이니 inverse 는 간단히 p = T^-1P로 계산할 수 있습니다.


위와 같은 계산들로 와핑을 할 수 있는데요.
그런데 2x2 행렬로 translation(이동) 을 할 수가 있을까요?
안타깝지만 2x2 행렬 계산으로는 이동을 시킬 수가 없습니다.
이는 linear operation이 아니기 때문이죠.

2D Linear Transformations
첫번째 transformation 정리를 해보겠습니다.
할 수 있는 거
- 크기, 회전, 기울이기, 반전
특징
- 원점 매핑
- 선 매핑
- 평행선 유지
- 비율 유지
- 클로즈된 구성들 (연속 연산 가능)

2x2 행렬로 이렇게 많은 걸 할 수 있다니!
너무 편하고 좋습니다. 하지만 슬프게도 translation이 안됩니다..
이동 하나 때문에 linear transformation을 잃을 수 없다! 라는 관점에서 나온 게 Homogeneous coordinates 개념입니다.
Homogeneous coordinates
일종의 트릭으로 하나의 dimension을 늘리는 겁니다. 2차 도메인에 z축으로 1을 추가하는 예를 들어 봅시다.

이를 통해서 w라는 homogeneous plane 이라는 평면 위에 Projection을 해서 이 값들을 w 에 해당하는 값들로 나눠 주면 해당되면 새로운 x',y' 를 구할 수 있습니다. 여기서는 w = 1 입니다.


이 개념을 통해서 Translation을 구현할 수 있습니다.

이 때 T 행렬의 마지막 행은 무조건 0,0,1 로 구성되어야합니다.
이를 포함시키는 것이 affine transfomation 입니다.
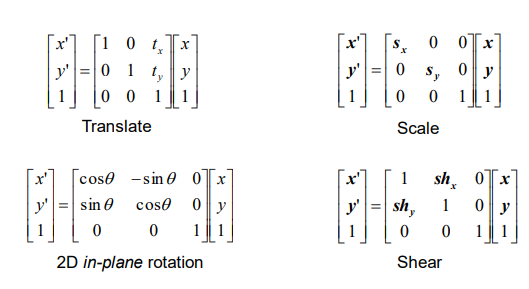
Affine Transfomation
할 수 있는 것
- linear transformation + Translations
특징
- 원점 유지 안됨 -> 이동을 하기 때문에
- 선 매핑
- 평행선 유지
- 비율 유지
- 클로즈된 구성들 (연속 연산 가능)

Projective Transformation
(Homographies이라고도 불림)
할 수 있는 거
- Affine transformation + Projective warp
특징
- 원점 매핑 x
- 선 매핑
- 평행 유지 x
- 비율 유지 x
- 클로즈된 구성들
이는 affine transfomation에서 3x3 행렬 중 마지막 행렬이 0, 0, 1 이 아닐 때 사용가능합니다.
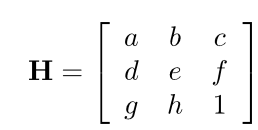
이는 Projective 가 가능합니다. 다음과 간은 Perspective 가 가능한 것이죠.

아래의 표를 보면서 정리하구 어떤 transformation이 어떤 특징이 있는지 다시 생각해보시면 도움이 많이 될 거 같습니다.

오늘은 linear transformation, affine transformation, projective transformation과 image warping에 대해 배워보았습니다.
'공부 > 컴퓨터비젼' 카테고리의 다른 글
| [컴퓨터비젼] 9. RANSAC (0) | 2021.04.12 |
|---|---|
| Canny Edge 설명 & 구현코드 (0) | 2021.04.06 |
| [컴퓨터비젼] 8. Image alignment (0) | 2021.04.05 |
| [컴퓨터비젼] 6. Feature descriptors and matching (2) | 2021.03.29 |
| [컴퓨터비젼] 5. Corner Detection와 Harris Operator (2) | 2021.03.29 |



