Arithmetic & Logic Unit (ALU)
- 컴퓨터 내에서의 정수 연산
- floating point(실수) 표현
- 과거에는 Co-processor

Control Unit 에는 제어 신호가 들어갑니다. Flags 는 오버플로우 등의 신호가 나옵니다.
Sigh-Magnitude(부호와 절댓값으로 표현)
가장 왼쪽 부호(LSB)가 양수,음수를 나타내는 bit 입니다.

이거에 단점은 +0 , -0 처럼 0의 표현식이 두개 입니다. 또 연산 후 부호를 다시 판단 해야함으로 불편합니다.
그래서 2의 보수법이 나왔습니다.

0이 단 하나의 표현식이 있습니다.
간단히 2의 보수를 음수로 바꾸는 법에 대해 말하자면

식을 0->1 ,1->0 로 반전시키고

+1 을 해주면 됩니다. (-3)
이 2의 보수를 가지고 하드워어적인 덧셈기와 뺄셈기를 보겠습니다.
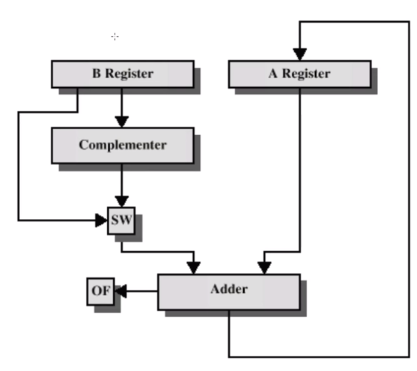
보면 뺄셈기가 없습니다. 뺄셈기는 덧셈기를 활용하면 되기 때문에 없습니다. ( a - b = a + (-b))

곱셈기는 좀 복잡합니다.

이 식으로 좀 더 쉽게 구할 수 있는 회로가 있습니다.
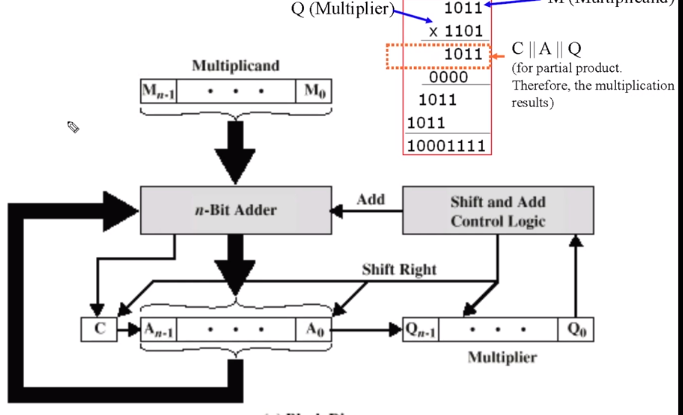


4비트 + 4비트를 하면 5비트가 나옵니다. 즉 가장 큰 자리수의 값은 Carry 에 읽을 겁니다 .
실행 예시

C는 캐리고 A 는 덧셈의 결과가 나오는 부분입니다.
Multiplier 에 마지막 비트가 색칠되어 있는데 이건 뭘까요?

이 하위 비트 만을 보고 있습니다. (곱셈을 해야하고 쉬프트 해줘야하니깐요)

Q 의 전체 값입니다. 숫자가 보이지 않나요?

Multiplier 입니다. 이 계산을 다하면 multiplier가 쉬프트 레프트가 다 되면

이렇게 값이 사라집니다.
그럼 이제 1011 x 1101 을 해보겠습니다. '1101 '의 1을 1011 와 곱해주어야합니다. Q0이 1이기 때문에
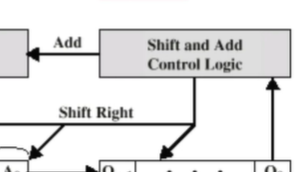
add 를 하게 됩니다.(나중에 shift 도 진행됩니다)


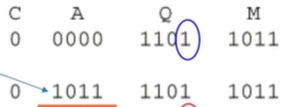
그리고 쉬프트가 됩니다.

다음 Q1 은 0이기 때문에 add 말고 shift 만 해두면 됩니다.


마지막의 Q A 값이 연산의 결과와 동일한 것을 볼 수 있습니다.
이 회로가 굉장히 효율적인 걸 볼 수 있습니다. 결과를 다른 위치가 아니였기 때문입니다.
이걸로 음수 계산도 가능할까요? 그건 불가능합니다.
Real Numbers
실수가 컴퓨터 상에서 어떻게 표현이 되는지 알아보겠습니다 .

Floating Point

biased exponent 에서 -127 을 해주어야 의도한 값이 나옵니다.


127을 기준으로 크면 양수 작으면 음수로 구분하기 위해서 이렇게 해줍니다.
'공부 > 컴퓨터 구조' 카테고리의 다른 글
| 컴퓨터구조11 Instruction Sets : Addressing Modes and Formats (0) | 2020.06.30 |
|---|---|
| 컴퓨터구조10 Instruction Sets : Characteristics and Functions (0) | 2020.06.29 |
| 컴퓨터구조7 Input/Output (0) | 2020.06.22 |
| 컴퓨터구조6 External Memory (0) | 2020.06.13 |
| 컴퓨터구조5 Internal Memory (0) | 2020.06.12 |



