알고리즘 중간고사 대비 자료 정리

#include <stdio.h>
//recursive로 구현한 피보나치 수열
//장점 : 구현 간단, 직관적
//단점 : The recursive algorithm hits all these nodes! 
int fib(int n){
		if(n<= 1)
			return n;
		else
			return fib(n-1) + fib(n-2);
	}
    
    
//Iterative version
//Fills array from left to right
//very efficient!
int fib2(int n){
	int i;
	int f[n];
	f[0]=0;
	if(n>0){
		f[1]=1;
		for(i=2;i<=n;i++)
			f[i] = f[i-1]+f[i-2];
	}
	
	for(i=0;i<=n;i++)
		printf("%d ",*(f+i));
}

int main(){
	int n = 10;
	int i;
	for(i=0;i<10;i++)
		printf("fib(%d) : %d\n",i,fib(i));
		
	fib2(10);
}

 

 

-Analysis of algorithms

1.Time complexity

2.Efficiency

 

Time Complexity 예시 함수들

 

1. 시간 복잡도 : 상수

n에 관계없이 상수 시간

fucntion1(a[],n){
	k = n/2;
    return a[k];
}
->Constant time regardless of n

 

2. 시간 복잡도 : n

function2(a[],n){
	sum <- 0;
    for i <- 1 to n
    	sum <- sum+ a[i];
    return sum;
}
->time is propotional to n

3. 시간 복잡도 : n^2

function3(a[],n){
	sum<-0;
    for i<-1 to n
    	for j <-1 to n
        	sum <- sum + a[i]*a[j];
    return sum;
}
->time is proportional to n^2

 

 

 

-Types of complexity

1. Worst case(our main focus) 

2. Best case

3. Average case

 

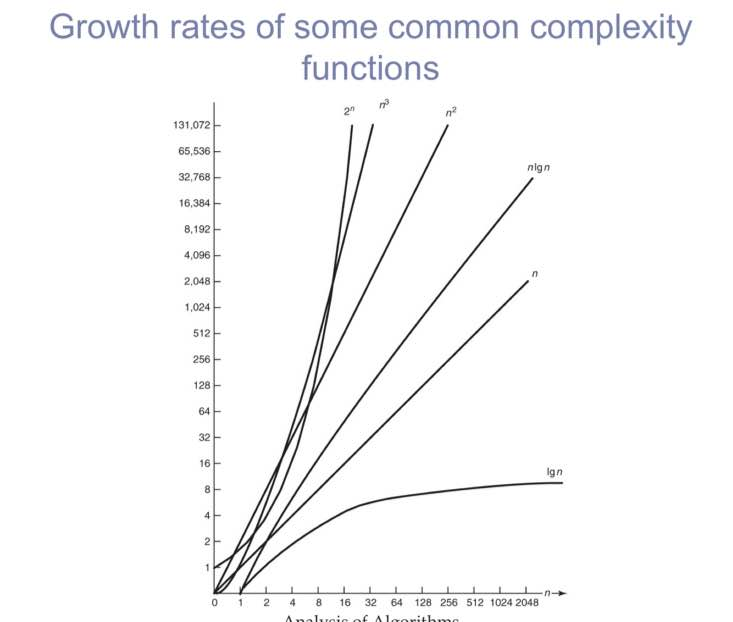
-Big O

Definition

:For a given complexity function f(n), O(f(n)) is the set of functions g(n) for which there exists some positive real constant c and some nonnegative integer N such that for all n>= N,

 

g(n)<= c x f(n)